
3.功率的计算式:P=Fvcosθ,其中θ是力与速度间的夹角。该公式有两种用法:①求某一时刻的瞬时功率。这时F是该时刻的作用力大小,v取瞬时值,对应的P为F在该时刻的瞬时功率;②当v为某段位移(时间)内的平均速度时,则要求这段位移(时间)内F必须为恒力,对应的P为F在该段时间内的平均功率。
2.功率的定义式: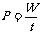 ,所求出的功率是时间t内的平均功率。
,所求出的功率是时间t内的平均功率。
1.功率的物理意义:功率是描述做功快慢的物理量。
3.了解常见力做功的特点:
重力(或电场力)做功和路径无关,只与物体始末位置的高度差h(或电势差)有关:W=mgh(或W=qU),当末位置低于初位置时,W>0,即重力做正功;反之则重力做负功。
滑动摩擦力做功与路径有关。当某物体在一固定平面上运动时,滑动摩擦力做功的绝对值等于摩擦力与路程的乘积。
在弹性范围内,弹簧做功与始末状态弹簧的形变量有关系。
2.会判断正功、负功或不做功。判断方法有:1用力和位移的夹角α判断;2用力和速度的夹角θ判断定;3用动能变化判断.
1.功是力的空间积累效应。它和位移相对应。计算功的方法有两种:
⑴按照定义求功。即:W=Fscosθ。 在高中阶段,这种方法只适用于恒力做功。当 时F做正功,当
时F做正功,当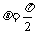 时F不做功,当
时F不做功,当 时F做负功。
时F做负功。
这种方法也可以说成是:功等于恒力和沿该恒力方向上的位移的乘积。
⑵用动能定理W=ΔEk或功能关系求功。当F为变力时,高中阶段往往考虑用这种方法求功。
这种方法的依据是:做功的过程就是能量转化的过程,功是能的转化的量度。如果知道某一过程中能量转化的数值,那么也就知道了该过程中对应的功的数值。
14.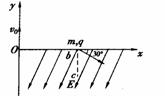 如图所示,一质量为m,带电荷量为+q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从点b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强为E、方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方的c点,如图所示。粒子的重力不计,试求:
如图所示,一质量为m,带电荷量为+q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从点b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强为E、方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方的c点,如图所示。粒子的重力不计,试求:
(1)圆形匀强磁场的最小面积。
13.如图所示,一质量为m、电量为+q的带电小球以与水平方向成某一角度θ的初速度v0射入水平方向的匀强电场中,小球恰能在电场中做直线运动.若电场的场强大小不变,方向改为相反同时加一垂直纸面向外的匀强磁场,小球仍以原来的初速度重新射人,小球恰好又能做直线运动.求电场强度的大小、磁感应强度的大小和初速度与水平方向的夹角θ。

12.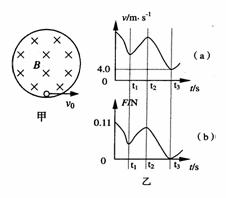 竖直平面内有一圆形绝缘轨道,半径R=0.4 m,匀强磁场垂直于轨道平面向里,质量m = 1×10-3 kg、带电量q =+3×10-2 C的小球,可在内壁滑动,如图甲所示.在轨道的最低点处给小球一个初速度v0,使小球在竖直平面内逆时针做圆周运动,图乙(a)是小球做圆周运动的速率v随时间变化的情况,图乙(b)是小球所受轨道的弹力F随时间变化的情况,结合图像所给数据,(g = 10 m/s2)求:(1)匀强磁场的磁感应强度;(2)小球的初速度v0.
竖直平面内有一圆形绝缘轨道,半径R=0.4 m,匀强磁场垂直于轨道平面向里,质量m = 1×10-3 kg、带电量q =+3×10-2 C的小球,可在内壁滑动,如图甲所示.在轨道的最低点处给小球一个初速度v0,使小球在竖直平面内逆时针做圆周运动,图乙(a)是小球做圆周运动的速率v随时间变化的情况,图乙(b)是小球所受轨道的弹力F随时间变化的情况,结合图像所给数据,(g = 10 m/s2)求:(1)匀强磁场的磁感应强度;(2)小球的初速度v0.
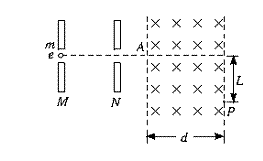
11.电子自静止开始经M、N板间(两板间的电压为u)的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.(已知电子的质量为m,电量为e)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com