
1.根据学生的实际,有针对性地进行复习,提高复习的有效性.由于解析几何通常有2-3小题和1大题,约占28分左右,而小题以考查基础为主、解答题的第一问也较容易,因此,对于全市的所有不同类型的学校,都要做好该专题的复习,千万不能认为该部分内容较难而放弃对该部分内容的专题复习,并且根据生源状况有针对性地进行复习,提高复习的有效性.
(十)轨迹方程
⑴ 曲线上的点的坐标都是这个方程的解;
⑵ 以这个方程的解为坐标的点都是曲线上的点.
那么,这个方程叫做曲线的方程;这条曲线叫做方程的曲线(图形或轨迹).
(九)抛物线的标准方程和几何性质
1.抛物线的定义:平面内到一定点(F)和一条定直线(l)的距离相等的点的轨迹叫抛物线。这个定点F叫抛物线的焦点,这条定直线l叫抛物线的准线。
需强调的是,点F不在直线l上,否则轨迹是过点F且与l垂直的直线,而不是抛物线。
2.抛物线的方程有四种类型:
 、
、 、
、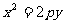 、
、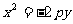 .
.
对于以上四种方程:应注意掌握它们的规律:曲线的对称轴是哪个轴,方程中的该项即为一次项;一次项前面是正号则曲线的开口方向向x轴或y轴的正方向;一次项前面是负号则曲线的开口方向向x轴或y轴的负方向。
3.抛物线的几何性质,以标准方程y2=2px为例
(1)范围:x≥0;
(2)对称轴:对称轴为y=0,由方程和图像均可以看出;
(3)顶点:O(0,0),注:抛物线亦叫无心圆锥曲线(因为无中心);
(4)离心率:e=1,由于e是常数,所以抛物线的形状变化是由方程中的p决定的;
(5)准线方程 ;
;
(6)焦半径公式:抛物线上一点P(x1,y1),F为抛物线的焦点,对于四种抛物线的焦半径公式分别为(p>0):

(7)焦点弦长公式:对于过抛物线焦点的弦长,可以用焦半径公式推导出弦长公式。设过抛物线y2=2px(p>O)的焦点F的弦为AB,A(x1,y1),B(x2,y2),AB的倾斜角为α,则有①|AB|=x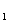 +x
+x +p
+p
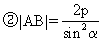
以上两公式只适合过焦点的弦长的求法,对于其它的弦,只能用“弦长公式”来求。
(8)直线与抛物线的关系:直线与抛物线方程联立之后得到一元二次方程:x +bx+c=0,当a≠0时,两者的位置关系的判定和椭圆、双曲线相同,用判别式法即可;但如果a=0,则直线是抛物线的对称轴或是和对称轴平行的直线,此时,直线和抛物线相交,但只有一个公共点。
+bx+c=0,当a≠0时,两者的位置关系的判定和椭圆、双曲线相同,用判别式法即可;但如果a=0,则直线是抛物线的对称轴或是和对称轴平行的直线,此时,直线和抛物线相交,但只有一个公共点。
(八)双曲线的简单几何性质
1.双曲线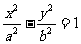 的实轴长为2a,虚轴长为2b,离心率
的实轴长为2a,虚轴长为2b,离心率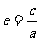 >1,离心率e越大,双曲线的开口越大.
>1,离心率e越大,双曲线的开口越大.
2. 双曲线 的渐近线方程为
的渐近线方程为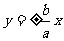 或表示为
或表示为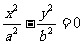 .若已知双曲线的渐近线方程是
.若已知双曲线的渐近线方程是 ,即
,即 ,那么双曲线的方程具有以下形式:
,那么双曲线的方程具有以下形式:
 ,其中k是一个不为零的常数.
,其中k是一个不为零的常数.
3.双曲线的第二定义:平面内到定点(焦点)与到定直线(准线)距离的比是一个大于1的常数(离心率)的点的轨迹叫做双曲线.对于双曲线 ,它的焦点坐标是(-c,0)和(c,0),与它们对应的准线方程分别是
,它的焦点坐标是(-c,0)和(c,0),与它们对应的准线方程分别是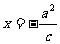 和
和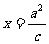 .
.
在双曲线中,a、b、c、e四个元素间有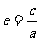 与
与 的关系,与椭圆一样确定双曲线的标准方程只要两个独立的条件.
的关系,与椭圆一样确定双曲线的标准方程只要两个独立的条件.
(七)双曲线及其标准方程
1.双曲线的定义:平面内与两个定点 、
、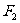 的距离的差的绝对值等于常数2a(小于|
的距离的差的绝对值等于常数2a(小于|
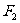 |)的动点
|)的动点 的轨迹叫做双曲线.在这个定义中,要注意条件2a<|
的轨迹叫做双曲线.在这个定义中,要注意条件2a<|
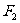 |,这一条件可以用“三角形的两边之差小于第三边”加以理解.若2a=|
|,这一条件可以用“三角形的两边之差小于第三边”加以理解.若2a=|
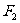 |,则动点的轨迹是两条射线;若2a>|
|,则动点的轨迹是两条射线;若2a>|
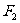 |,则无轨迹.
|,则无轨迹.
若 <
< 时,动点
时,动点 的轨迹仅为双曲线的一个分支,又若
的轨迹仅为双曲线的一个分支,又若 >
> 时,轨迹为双曲线的另一支.而双曲线是由两个分支组成的,故在定义中应为“差的绝对值”.
时,轨迹为双曲线的另一支.而双曲线是由两个分支组成的,故在定义中应为“差的绝对值”.
2. 双曲线的标准方程: 和
和 (a>0,b>0).这里
(a>0,b>0).这里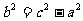 ,其中|
,其中|
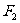 |=2c.要注意这里的a、b、c及它们之间的关系与椭圆中的异同.
|=2c.要注意这里的a、b、c及它们之间的关系与椭圆中的异同.
3.双曲线的标准方程判别方法是:如果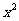 项的系数是正数,则焦点在x轴上;如果
项的系数是正数,则焦点在x轴上;如果 项的系数是正数,则焦点在y轴上.对于双曲线,a不一定大于b,因此不能像椭圆那样,通过比较分母的大小来判断焦点在哪一条坐标轴上.
项的系数是正数,则焦点在y轴上.对于双曲线,a不一定大于b,因此不能像椭圆那样,通过比较分母的大小来判断焦点在哪一条坐标轴上.
4.求双曲线的标准方程,应注意两个问题:⑴ 正确判断焦点的位置;⑵ 设出标准方程后,运用待定系数法求解.
(六)椭圆的参数方程
椭圆 (
(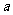 >
>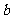 >0)的参数方程为
>0)的参数方程为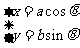 (θ为参数).
(θ为参数).
说明 ⑴ 这里参数θ叫做椭圆的离心角.椭圆上点P的离心角θ与直线OP的倾斜角α不同: ;
;
⑵ 椭圆的参数方程可以由方程 与三角恒等式
与三角恒等式 相比较而得到,所以椭圆的参数方程的实质是三角代换.
相比较而得到,所以椭圆的参数方程的实质是三角代换.
(五)椭圆的简单几何性质
1.椭圆的几何性质:设椭圆方程为 (
(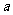 >
>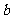 >0).
>0).
⑴ 范围: -a≤x≤a,-b≤x≤b,所以椭圆位于直线x= 和y=
和y= 所围成的矩形里.
所围成的矩形里.
⑵ 对称性:分别关于x轴、y轴成轴对称,关于原点中心对称.椭圆的对称中心叫做椭圆的中心.
⑶ 顶点:有四个 (-a,0)、
(-a,0)、 (a,0)
(a,0)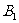 (0,-b)、
(0,-b)、 (0,b).
(0,b).
线段
 、
、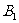
 分别叫做椭圆的长轴和短轴.它们的长分别等于2a和2b,a和b分别叫做椭圆的长半轴长和短半轴长. 所以椭圆和它的对称轴有四个交点,称为椭圆的顶点.
分别叫做椭圆的长轴和短轴.它们的长分别等于2a和2b,a和b分别叫做椭圆的长半轴长和短半轴长. 所以椭圆和它的对称轴有四个交点,称为椭圆的顶点.
⑷ 离心率:椭圆的焦距与长轴长的比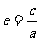 叫做椭圆的离心率.它的值表示椭圆的扁平程度.0<e<1.e越接近于1时,椭圆越扁;反之,e越接近于0时,椭圆就越接近于圆.
叫做椭圆的离心率.它的值表示椭圆的扁平程度.0<e<1.e越接近于1时,椭圆越扁;反之,e越接近于0时,椭圆就越接近于圆.
2.椭圆的第二定义
⑴ 定义:平面内动点M与一个顶点的距离和它到一条定直线的距离的比是常数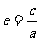 (e<1=时,这个动点的轨迹是椭圆.
(e<1=时,这个动点的轨迹是椭圆.
⑵ 准线:根据椭圆的对称性, (
(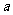 >
>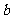 >0)的准线有两条,它们的方程为
>0)的准线有两条,它们的方程为 .对于椭圆
.对于椭圆 (
(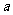 >
>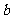 >0)的准线方程,只要把x换成y就可以了,即
>0)的准线方程,只要把x换成y就可以了,即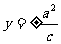 .
.
(四)椭圆及其标准方程
1.
椭圆的定义:椭圆的定义中,平面内动点与两定点 、
、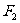 的距离的和大于|
的距离的和大于|
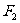 |这个条件不可忽视.若这个距离之和小于|
|这个条件不可忽视.若这个距离之和小于|
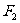 |,则这样的点不存在;若距离之和等于|
|,则这样的点不存在;若距离之和等于|
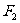 |,则动点的轨迹是线段
|,则动点的轨迹是线段
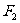 .
.
2.椭圆的标准方程: (
(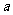 >
>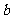 >0),
>0), (
(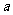 >
>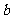 >0).
>0).
3.椭圆的标准方程判别方法:判别焦点在哪个轴只要看分母的大小:如果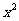 项的分母大于
项的分母大于 项的分母,则椭圆的焦点在x轴上,反之,焦点在y轴上.
项的分母,则椭圆的焦点在x轴上,反之,焦点在y轴上.
4.求椭圆的标准方程的方法:⑴ 正确判断焦点的位置;⑵ 设出标准方程后,运用待定系数法求解.
(四)圆的有关问题
1.圆的标准方程
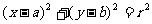 (r>0),称为圆的标准方程,其圆心坐标为(a,b),半径为r.
(r>0),称为圆的标准方程,其圆心坐标为(a,b),半径为r.
特别地,当圆心在原点(0,0),半径为r时,圆的方程为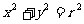 .
.
2.圆的一般方程
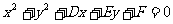 (
( >0)称为圆的一般方程,
>0)称为圆的一般方程,
其圆心坐标为( ,
, ),半径为
),半径为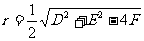 .
.
当 =0时,方程表示一个点(
=0时,方程表示一个点( ,
, );
);
当 <0时,方程不表示任何图形.
<0时,方程不表示任何图形.
(三)线性规划问题
1.线性规划问题涉及如下概念:
⑴存在一定的限制条件,这些约束条件如果由x、y的一次不等式(或方程)组成的不等式组来表示,称为线性约束条件.
⑵都有一个目标要求,就是要求依赖于x、y的某个函数(称为目标函数)达到最大值或最小值.特殊地,若此函数是x、y的一次解析式,就称为线性目标函数.
⑶求线性目标函数在线性约束条件下的最大值或最小值问题,统称为线性规划问题.
⑷满足线性约束条件的解(x,y)叫做可行解.
⑸所有可行解组成的集合,叫做可行域.
⑹使目标函数取得最大值或最小值的可行解,叫做这个问题的最优解.
2.线性规划问题有以下基本定理:
⑴ 一个线性规划问题,若有可行解,则可行域一定是一个凸多边形.
⑵ 凸多边形的顶点个数是有限的.
⑶ 对于不是求最优整数解的线性规划问题,最优解一定在凸多边形的顶点中找到.
3.线性规划问题一般用图解法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com