13.若A＝{x∈R||x|<3}，B＝{x∈R|2^x>1}，则A∩B＝　　.

解析：∵A＝{x|－3<x<3}，B＝{x|x>0}，

∴A∩B＝{x|0<x<3}.

答案：{x|0<x<3}

12.命题“∃两个向量p、q，使得|p·q|＝|p|·|q|”的否定是　　.

答案：∀两个向量p、q，均有|p·q|≠|p|·|q|

11．(2010·海口模拟)已知集合A＝{x∈R|＜2^x＜8}，B＝{x∈R|－1＜x＜m+1}，若x∈B成立的一个充分不必要的条件是x∈A，则实数m的取值范围是________．

解析：A＝{x∈R|＜2^x＜8}

＝{x|－1＜x＜3}，

∵x∈B成立的一个充分不必要条件是x∈A，

∴AB，

∴m+1＞3，即m＞2.

答案：(2，+∞)

10.已知p：－1≤4x－3≤1，q：x²－(2a+1)x+a(a+1)≤0，若　 p是　 q的必要不充分

条件，则实数a的取值范围是　　　　　　　　　　　　　　　　　　　 　(　)

A.[0，] 　　　　　B.[，1]　　　　　 C.[，]　 　　　　　　D.(，1]

解析：由题知，p为M＝[，1]，q为N＝[a，a+1].

∵　 p是　 q的必要不充分条件，∴p是q的充分不必要条

件，从而有MN于是可得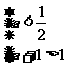.而且当a=0或a=

时，同样满足MN 成立故a的取值范围是[0,]　

答案：A

第Ⅱ卷　(非选择题，共100分)

9.(2010·马鞍山质检)给出下列结论：

①命题“若p，则q或r”的否命题是“若　 p，则　 q且　 r”；

②命题“若　 p，则q”的逆否命题是“若p，则　 q”；

③命题“∃n∈N^*，n²+3n能被10整除”的否命题是“∀n∈N^*，n²+3n不能被10整除”；

④命题“∀x，x²－2x+3>0”的否命题是“∃x，x²－2x+3<0”.

其中正确结论的个数是　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.1　 　　　　B.2　　　　 C.3　 　　　　　D.4

解析：由于否命题是把原命题的否定了的条件作条件、否定了的结论作结论得到的命题，故①正确；由于逆否命题是把原命题的否命题了的结论作条件、否定了的条件作结论得到的命题，故②不正确；特称命题的否命题是全称命题，故③正确；虽然全称命题的否命题是特称命题，但对结论的否定错误，故④不正确.

答案：B

8.“a＝b”是“直线y＝x+2与圆(x－a)²+(y－b)²＝2相切”的　　　　　　　 (　)

A.充分不必要条件　　　　　　　 　B.必要不充分条件

C.充要条件　 　　　　　　　　　　　D.既不充分也不必要条件

解析：a＝b时，圆心到直线距离d＝＝，所以相切，若直线与圆相切时，有d＝＝，所以a＝b或a＝－4+b.

答案：A

7.已知a，b为实数，则2^a>2^b是log₂a>log₂b的　　　　　　　　　　　　　　　　 (　)

A.充分而不必要条件　　　　　　　　 B.必要而不充分条件

C.充要条件　　　　　　　　　　　　 D.既不充分也不必要条件

解析：p：2^a>2^b⇔a>b；q：log₂a>log₂b⇔a>b>0，

故pq，q⇒p，∴p是q的必要不充分条件.

答案：B

6.下列特称命题中，假命题是　　　　　　　　　　　　　　　　　　　　 (　)

A.∃x∈R，x²－2x－3＝0　　　　　　　 　B.至少有一个x∈Z，x能被2和3整除

C.存在两个相交平面垂直于同一直线　　　 D.∃x∈{x|x是无理数}，使x²是有理数

解析：对于A：当x＝－1时，x²－2x－3＝0，故A为真命题；

对于B：当x＝6时，符合题目要求，为真命题；

对于C假命题；

对于D：x＝时，x²＝3，故D为真命题.

综上可知：应选C.

答案：C

5.已知a，b是实数，则“a>0且b>0”是“a+b>0且ab>0”的　　　　　　　 (　)

A.充分而不必要条件　 　　　　　　　　B.必要而不充分条件

C.充分必要条件 　　　　　　　　　　　D.既不充分也不必要条件

解析：当a>0且b>0时，一定有a+b>0且ab>0.反之，当a+b>0且ab>0时，一定有a>0，b>0.故“a>0且b>0”是“a+b>0且ab>0”的充要条件.

答案：C

4.已知命题p：x∈A∪B，则　 p是　 　　　　　　　　　　　　　　　　　　(　)

A.x∉A∩B　 　　　　B.x∉A或x∉B　　　 C.x∉A且x∉B　 　　　　D.x∈A∩B

解析：由x∈A∪B知x∈A或x∈B.

答案：C