
9.已知f(x)=ax,g(x)=logax(a>0,且a≠1),若f(3)·g(3)<0,那么f(x)与g(x)在同一坐标系内的图象可能是 ( )

解析:首先清楚这两类函数图象在坐标系中的位置和走向,另外还应知道f(x)=ax与g(x)=logax(a>0,且a≠1)互为反函数,于是可排除A、D.因图中B、C关于y=x对称,最后利用函数值关系式f(3)·g(3)<0,排除B,故选C .
答案:C
8.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是 ( )

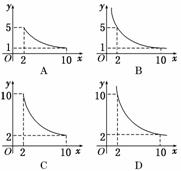
解析:由题意可知,y=(2≤x≤10).
答案:A
7.若函数f(x)=x3+f′(1)x2-f′(2)x+3,则f(x)在点(0,f(0))处切线的倾斜角为 ( )
A. B. C. D.
解析:由题意得:f′(x)=x2+f′(1)x-f′(2),
令x=0,得f′(0)=-f′(2),
令x=1,得f′(1)=1+f′(1)-f′(2),
∴f′(2)=1,∴f′(0)=-1,
即f(x)在点(0,f(0))处切线的斜率为-1,
∴倾斜角为π.
答案:D
6.下列是关于函数y=f(x),x∈[a,b]的几个命题:
①若x0∈[a,b]且满足f(x0)=0,则(x0,0)是f(x)的一个零点;
②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
③函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
④用二分法求方程的根时,得到的都是近似值.
那么以上叙述中,正确的个数为 ( )
A.0 B.1 C.3 D.4
解析:因为①中x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点,而不是(x0,0),所以①错误;
②因为函数f(x)不一定连续,所以②错误;
③方程f(x)=0的根一定是函数f(x)的零点,所以③错误;
④用二分法求方程的根时,得到的根也可能是精确值,所以④也错误.
答案:A
5.函数f(x)=lg 的大致图象是
( )
的大致图象是
( )
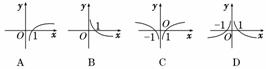
解析:∵f(x)=lg =lg是偶函数,
=lg是偶函数,
∴A、B不正确.
又∵当x>0时,f(x)为增函数,
∴D不正确.
答案:C
4.下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,+∞)上是减函数;(3)是偶函数.这样的函数是 ( )
A.y=x3+1 B.y=log2(|x|+2) C.y=()|x| D.y=2|x|
解析:显然四个函数都满足性质(1),而满足性质(2)的只有C.
答案:C
3.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a= ( )
A.2 B.3 C.4 D.5
解析:因为f(x)在x=-3时取得极值,故x=-3是f′(x)=3x2+2ax+3=0的解,代入得a=5.
答案:D
2.设 ( )
( )
A. B. C.- D.
解析:f(f())=f(-)=.
答案:B
1.化简[(-2)6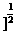 -(-1)0的结果为
( )
-(-1)0的结果为
( )
A.-9 B.7 C.-10 D.9
解析:[(-2)6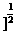 -(-1)0=(26
-(-1)0=(26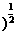 -1=8-1=7.
-1=8-1=7.
答案:B
21.(本小题满分14分)看下面的问题:1+2+3+…+( )>10 000这个问题的答案虽然不唯一,但是我们只要确定出满足条件的最小正整数n0,括号内填写的数字只要大于或等于n0即可.试写出寻找满足条件的最小正整数n0的算法并画出相应的程序框图.
解:算法一:第一步,p=0;
第二步,i=0;
第三步,i=i+1;
第四步,p=p+i;
第五步,如果p>10 000,则输出i,否则,执行第六步;
第六步,回到第三步,重新执行第三步,第四步,第五步.
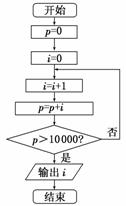
该算法的程序框图如图所示:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com