5．某公共汽车站每隔5分钟有一辆车通过(假设每一辆带走站上的所有乘客)，乘客到达汽车站的时间是任意的，则乘客候车时间不超过3分钟的概率为　　　　　　　 (　)

A.　 　　　　　　　B.　　　　　　　　　 C. 　　　　　　D.

解析：P＝＝.

答案：B

4．两个骰子的点数分别为b、c，则方程x²+bx+c＝0有两个实根的概率为　 (　)

A.　 　　　　　B.　　　　　　　　　　 C. 　　　　　　D.

解析：共有36个结果，方程有解，则Δ＝b²－4c≥0，∴b²≥4c，满足条件的数记为(b^2,4c)，共有(4,4)，(9,4)，(9,8)，(16,4)，(16,8)，(16,12)，(16,16)，(25,4)，(25,8)，(25,12)，(25,16)，(25,20)，(25,24)，(36,4)，(36,8)，(36,12)，(36,16)，(36,20)，(36,24),19个结果，P＝.

答案：C

3．在△ABC中，D是BC的中点，向△ABC内任投一点．那么点落在△ABD内的概为(　)

A.　　　　　B.　　　　　　　 C. 　　　　　　　　　　D.

解析：因为D是BC的中点，所以S_△ABD＝S_△ABC，

所以点落在△ABD内的概率为.

答案：B

2．有四个游戏盘，如果撒一粒黄豆落在阴影部分，则可中奖，小明希望中奖，他应当选择的游戏盘为　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　(　)

解析：A游戏盘的中奖概率为，B游戏盘的中奖概率为，C游戏盘的中奖概率为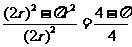，D游戏盘的中奖概率为 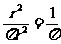，A游戏盘的中奖概率最大．

答案：A

1．把红桃、黑桃、方块、梅花四张纸牌随机发给甲、乙、丙、丁四个人，每人分得一张，事件“甲分得梅花”与事件“乙分得梅花”是　　　 　　　　　　　　　　　(　)

A．对立事件　　　 　B．不可能事件

C．互斥但不对立事件　　 　D．以上答案均不对

解析：四张纸牌分发给四人，每人一张，甲和乙不可能同时分得梅花，所以是互斥事件，但也有可能丙或丁分得梅花，故不是对立事件．

答案：C

21．(本小题满分14分)已知不等式x²+px+1＞2x+p.

(1)如果不等式当|p|≤2时恒成立，求x的范围；

(2)如果不等式当2≤x≤4时恒成立，求p的范围．

解：(1)原不等式为

(x－1)p+(x－1)²＞0，

令f(p)＝(x－1)p+(x－1)²，它是关于p的一次函数，

定义域为[－2,2]，由一次函数的单调性知

，

解得x＜－1或x＞3.

即x的取值范围是{x|x＜－1或x＞3}．

(2)不等式可化为(x－1)p＞－x²+2x－1，

∵2≤x≤4，∴x－1＞0.

∴p＞＝1－x.

对x∈[2,4]恒成立，

所以p＞(1－x)_max.

当2≤x≤4时，(1－x)_max＝－1，

于是p＞－1.故p的范围是{p|p＞－1}．

20．(本小题满分13分)某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”．该厂所用的主要原料为A、B两种贵金属，已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒，生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒．若奥运会标志每套可获利700元，奥运会吉祥物每套可获利1200元，该厂月初一次性购进原料A、B的量分别为200盒和300盒．问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大？最大利润为多少？

解：设该厂每月生产奥运会标志和奥运会吉祥物分别为x，y套，月利润为z元，

由题意得

目标函数为z＝700x+1200y.

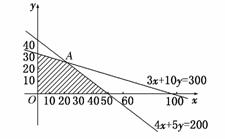
作出二元一次不等式组所表示的平面区域，即可行域，如图：

目标函数可变形为y＝－x+，

∵－＜－＜－，

∴当y＝x+通过图中的点A时，最大，z最大．解得点A坐标为(20,24)．

将点A(20,24)代入z＝700x+1200y

得z_max＝700×20+1200×24＝42800元．

答：该厂生产奥运会标志和奥运会吉祥物分别为20、24套时月利润最大，最大利润为42800元．

19．(本小题满分12分)已知函数f(x)＝ax²+4(a为非零实数)，设函数F(x)＝.

(1)若f(－2)＝0，求F(x)的表达式；

(2)设mn＜0，m+n＞0，试判断F(m)+F(n)能否大于0?

解：(1)由f(－2)＝0,4a+4＝0⇒a＝－1，

∴F(x)＝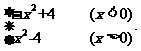

(2)∵，∴m，n一正一负．

不妨设m＞0且n＜0，则m＞－n＞0，

F(m)+F(n)＝f(m)－f(n)＝am²+4－(an²+4)

＝a(m²－n²)，

当a＞0时，F(m)+F(n)能大于0，

当a＜0时，F(m)+F(n)不能大于0.

18．(本小题满分12分)(2010·吉林模拟)沪杭高速公路全长166千米．假设某汽车从上海莘庄镇进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶到杭州．已知该汽车每小时的运输成本y(以元为单元)由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，比例系数为0.02；固定部分为200元．

(1)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；

(2)汽车应以多大速度行驶才能使全程运输成本最小？最小运输成本为多少元？

解：(1)依题意得：y＝(200+0.02v²)×

＝166(0.02v+)(60≤v≤120)．

(2)y＝166(0.02v+)≥166×2

＝664(元)

当且仅当0.02v＝即v＝100千米/时时取等号．

答：当速度为100千米/时时，最小的运输成本为664元．

17．(本小题满分12分)若a₁＞0，a₁≠1，a_n+1＝(n＝1,2，…)

(1)求证：a_n+1≠a_n；

(2)令a₁＝，写出a₂、a₃、a₄、a₅的值，观察并归纳出这个数列的通项公式a_n.

解：(1)证明：(采用反证法)．若a_n+1＝a_n，

即＝a_n，解得a_n＝0,1.

从而a_n＝a_n－1＝…＝a₂＝a₁＝0,1，与题设a₁＞0，a₁≠1相矛盾，

故a_n+1≠a_n成立．

(2)a₁＝、a₂＝、a₃＝、a₄＝、a₅＝，a_n＝，

n∈N^*.