
3.设P1(2,-1),P2(0,5),且P在P1P2的延长线上,使|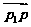 |=2|
|=2|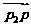 |,则点P为( )
|,则点P为( )
A.(-2,11) B.(,3) C.(,3) D.(2,-7)
解析:由题意知 =
=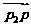 ,
,
设P(x,y),则(-2,6)=(x,y-5),
∴ ∴
∴
∴点P的坐标为(-2,11).
答案:A
2.有下列四个命题:
①(a·b)2=a2·b2; ②|a+b|>|a-b|;③|a+b|2=(a+b)2; ④若a∥b,则a·b=|a|·|b|.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
解析:①(a·b)2=|a|2·|b|2·cos2〈a,b〉
≤|a|2·|b|2=a2·b2;
②|a+b|与|a-b|大小不确定;
③正确;
④a∥b,则a=λb(λ∈R),∴a·b=λ·b2,
而|a|·|b|=|λ|·|b|·|b|=|λ|b2,
∴④不正确.
答案:A
1.设z=1+i(i是虚数单位),则+z2= ( )
A.-1-i B.-1+I C.1-i D.1+i
解析:+z2=+(1+i)2=+1+i2+2i=1+i.
答案:D
21.(本小题满分14分)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人中和B类工人中各抽查多少工人?
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
表1:
|
生产能 力分组 |
[100,110) |
[110,120) |
[120,130) |
[130,140) |
[140,150) |
|
人数 |
4 |
8 |
x |
5 |
3 |
表2:
|
生产能 力分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150) |
|
人数 |
6 |
y |
36 |
18 |
(i)先确定x,y,再完成下列频率分布直方图,就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)

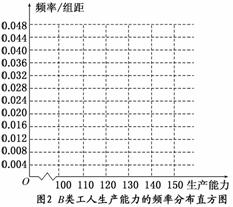
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
解:(1)A类工人中和B类工人中分别抽查25名和75名.
(2)(ⅰ)由4+8+x+5+3=25,得x=5,
6+y+36+18=75,得y=15.
频率分布直方图如下:


从直方图可以判断:B类工人中个体间的差异程度更小.
(ⅱ)  =
= ×105+
×105+ ×115+
×115+ ×125+
×125+ ×135+
×135+ ×145=123,
×145=123,
 =
= ×115+
×115+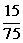 ×125+
×125+ ×135+
×135+ ×145=133.8,
×145=133.8,
 =
= ×123+
×123+ ×133.8=131.1.
×133.8=131.1.
A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.
20.(本小题满分12分)(2009·广东高考)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
|
API |
0-50 |
51-100 |
101-150 |
151-200 |
201-250 |
251-300 |
>300 |
|
级别 |
Ⅰ |
Ⅱ |
Ⅲ1 |
Ⅲ2 |
Ⅳ1 |
Ⅳ2 |
Ⅴ |
|
状况 |
优 |
良 |
轻微 污染 |
轻度 污染 |
中度污染 |
中度重 污染 |
重度 污染 |
|
|
 |
 |
 |
 |
 |
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
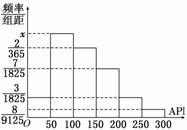
(1)求直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数.
解:(1)根据频率分布直方图可知,
x=÷50
=.
(2)空气质量为Y的天数=(Y对应的频率÷组距)×组距×365天,
所以一年中空气质量为良和轻微污染的天数分别是
×50×365=119(天)和×50×365=100(天).
0.275+0.100+0.050)×5 000=2 125;
(ii)平均分为:=85×0.025+95×0.050+105×0.200+115×0.300+125×0.275+135×0.100+145×0.050=117.5.
(iii)成绩落在[126,150]中的概率为:P=×0.275+0.10+0.050=0.260.
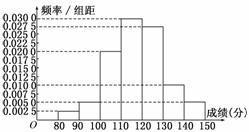
19.(本小题满分12分)某市十所重点中学进行高三联考,共有5 000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
|
分组 |
频数 |
频率 |
|
[80,90) |
① |
② |
|
[90,100) |
|
0.050 |
|
[100,110) |
|
0.200 |
|
[110,120) |
36 |
0.300 |
|
[120,130) |
|
0.275 |
|
[130,140) |
12 |
③ |
|
[140,150) |
|
0.050 |
|
合计 |
|
④ |
(1)根据上面频率分布表,推出①,②,③,④处的数值分别为 , , , ;
(2)在所给的坐标系中画出区间[80,150]上的频率分布直方图;
(3)根据题中信息估计总体:(i)120分及以上的学生数;
(ii)平均分;(iii)成绩落在[126,150]中的概率.
解:(1)①,②,③,④处的数值分别为:3,0.025,0.100,1.
(2)频率分布直方图如图所示
(3)(i)120分及以上的学生数为:
18.(本小题满分12分)在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y与腐蚀时间x的一组数据如下表所示:
|
x(秒) |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
|
y(微米) |
6 |
10 |
11 |
13 |
16 |
17 |
19 |
23 |
(1)画出数据的散点图;
(2)根据散点图,你能得出什么结论?
(3)求回归方程.
解:(1)散点图如图所示

(2)结论:x与y是具有相关关系的两个变量,且对应n组观测值的n个点大致分布在一条直线附近,其中整体上与这n个点最接近的一条直线最能代表变量x与y之间的关系.
(3)计算得r=0.979 307 992>0.75.所以,x与y有很强的线性相关关系,由计算器计算得 =6.616 438≈6.62,
=6.616 438≈6.62, =0.269 863≈0.27,
=0.269 863≈0.27,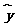 =6.62+0.27x.
=6.62+0.27x.
17.(本小题满分12分)已知数据x1,x2,…,x10的平均数=20,方差s2=0.015.求:
(1)3x1,3x2,…,3x10的平均数和方差;
(2)4x1-2,4x2-2,…,4x10-2的平均数和方差.
解:(1)′=(3x1+3x2+…+3x10)
=(x1+x2+…+x10)=3=3×20=60;
s′2=[(3x1-3)2+(3x2-3)2+…+(3x10-3)2]
=[(x1-)2+(x2-)2+…+(x10-)2]
=9s2=9×0.015=0.135.
(2)″=4-2=4×20-2=78;
s″2=16s2=16×0.015=0.24.
16.(本小题满分12分)某工厂人员及工资构成如表:
|
人员 |
经理 |
管理 人员 |
高级 技工 |
工人 |
学徒 |
合计 |
|
周工资 |
2 200 |
250 |
220 |
200 |
100 |
|
|
人数 |
1 |
6 |
5 |
10 |
1 |
23 |
|
合计 |
2 200 |
1 500 |
1 100 |
2 000 |
100 |
6 900 |
(1)指出这个问题中工资的众数、中位数、平均数;
(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么?
解:(1)众数200,中位数220,平均数300;
(2)平均数受数据中的极端值的影响较大,这个平均数是从一名工资极高(是工人工资的11倍)的经理和其他四类员工的周工资计算出来的,它不能客观地反映该工厂的工资水平.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com