10.设函数f(x)＝Asin(ωx+φ)，(A≠0，ω＞0，－＜φ＜)的图象关于直线x＝对称，它的周期是π，则　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.f(x)的图象过点(0，)　　　　　 B.f(x)的图象在[，]上递减

C.f(x)的最大值为A　　　　　　　 D.f(x)的一个对称中心是点(，0)

解析：T＝π，∴ω＝2.∵图象关于直线x＝对称，

∴sin(ω+φ)＝±1，

即×2+φ＝+kπ，k∈Z

又∵－<φ<，∴φ＝

∴f(x)＝Asin(2x+).再用检验法.

答案：D

第Ⅱ卷　(非选择题，共100分)

9.函数y＝sin(2x－)在区间[－，π]上的简图是　　　　　　　　　　　　　 (　)

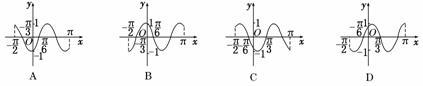
解析：当x＝－时，y＝sin(－π－)

＝sin＝＞0，排除B、D，

当x＝时，y＝sin(－)＝sin0＝0，排除C.

答案：A

8.设集合M＝{平面内的点(a，b)}，N＝{f(x)|f(x)＝acos2x+bsin2x，x∈R}，给出从M到N的映射f：(a，b)→f(x)＝acos2x+bsin2x，则点(1，)的象f(x)的最小正周期为(　)

A.π 　　　　　　B.　　　　　　　 C. 　　　　　　　　　D.

解析：f(x)＝cos2x+sin2x＝2sin(2x+)，则最小正周期为π.

答案：A

7.有一种波，其波形为函数y＝sin(x)的图象，若在区间[0，t]上至少有2个波峰(图象的最高点)，则正整数t的最小值是　　　　　　　　　　　　　　　　　　　　　　 (　)

A.3 　　　　　　　B.4　　　　　　　　 C.5　 　　　　　　D.6

解析：由T＝＝＝4，可知此波形的函数周期为4，显然当0≤x≤1时函数单调递增，x＝0时y＝0，x＝1时y＝1，因此自0开始向右的第一个波峰所对的x值为1，第二个波峰对应的x值为5，所以要区间[0，t]上至少两个波峰，则t至少为5.

答案：C

6.在△ABC中，若sin²A+sin²B－sinAsinB＝sin²C，且满足ab＝4，则该三角形的面积为(　)

A.1 　　　　B.2　　　　　　　　 C. 　　　　　　　　　D.

解析：∵sin²A+sin²B－sinAsinB＝sin²C，

∴a²+b²－ab＝c²，∴cosC＝＝，

∴C＝60°，∴S_△ABC＝absinC＝×4×＝.

答案：D

5.给定函数①y＝xcos(+x)，②y＝1+sin²(π+x)，③y＝cos(cos(+x))中，偶函数的个数

是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　(　)

A.3 　　　　　　　　B.2　　　　　　　　　 C.1 　　　　　　　　　　　　D.0

解析：对于①y＝xcos(π+x)＝xsinx，是偶函数，故①正确；对于②y＝1+sin²(π+x)＝sin²x+1，是偶函数，故②正确；对于③y＝cos(cos(+x))

＝cos(－sinx)＝cos(sinx)，

∵f(－x)＝cos(sin(－x))＝cos(－sinx)＝cos(sinx)＝f(x)，

∴函数是偶函数，故③正确.

答案：A

4.要得到y＝sin(2x－)的图象，只要将y＝sin2x的图象　　　　　　　　　　　 　(　)

A.向左平移个单位　 　　　　　　B.向右平移个单位

C.向左平移个单位　 　　　　　　D.向右平移个单位

解析：∵y＝sin(2x－)＝sin2(x－)，

∴只要将y＝sin2x的图象向右平移个单位便得到y＝sin(2x－)的图象.

答案：D

3.(2010·温州模拟)函数f(x)＝2sin(2x+)在[－，]上对称轴的条数为　　　　　 (　)

A.1 　　　　B.2　　　　　　　 C.3　 　　　　　　　　　D .0

解析：∵当－≤x≤，

∵－≤2x+≤π，

∴函数的对称轴为：2x+＝－，，

∴x＝－，或x＝.

答案：B

2.已知α∈(，π)，sinα＝，则tan(α+)等于　　　　　　　　　　　　　　　　 (　)

A. 　　　　　B.7　　　　　　 C.－ 　　　　　　　　D.－7

解析：由α∈(，π)，sinα＝，得tanα＝－，tan(α+)＝＝.

答案：A

1.集合M＝{x|x＝sin，n∈Z}，N＝{x|x＝cos，n∈N}，则M∩N等于　　　　 (　)

A.{－1,0,1}　　B.{0,1}　　　　　 C.{0} 　　　　　　　D.∅

解析：∵M＝{x|x＝sin，n∈Z}＝{－，0，}，

N＝{－1,0,1}，

∴M∩N＝{0}.

答案：C