12．已知极坐标系的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合．直线l的参数方程为(t为参数，θ为直线l的倾斜角)，圆C的极坐标方程为ρ²－8ρcosθ+12＝0.

(1)若直线l与圆C相切，求θ的值；

(2)若直线l与圆C有公共点，求θ的取值范围．

解：因为直线l的直角坐标方程为y=xtanθ或x=0，圆C的直角坐标方程为(x-4)²+y²=4.

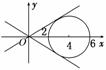由图形可知：

(1)当直线l与圆C相切时，θ=或θ=；

(2)当直线l与圆C有公共点时，θ∈[0，]∪[，π)．

11．已知直线l的参数方程：(t为参数)和圆C的极坐标方程：ρ＝2sin(θ+)(θ为参数)．

(1)将直线l的参数方程和圆C的极坐标方程化为直角坐标方程；

(2)判断直线l和圆C的位置关系．

解：(1)消去参数t，得直线l的直角坐标方程为y＝2x+1；

ρ＝2sin(θ+)即ρ＝2(sinθ+cosθ)，

两边同乘以ρ得ρ²＝2(ρsinθ+ρcosθ)，

消去参数θ，得⊙C的直角坐标方程为：

(x－1)²+(y－1)²＝2.

(2)圆心C到直线l的距离

d＝＝＜，

所以直线l和⊙C相交．

10．(2009·南京模拟)过点P(－3,0)且倾斜角为30°的直线和曲线(t为参数)相交于A、B两点，求线段AB的长．

解：曲线的普通方程为x²－y²＝4.

过点P(－3,0)且倾斜角为30°的直线方程为y＝x+，

联立方程组消去y得，

x²－2x－7＝0，

∴x₁x₂＝－.x₁+x₂＝3，

∴AB＝|x₁－x₂|

＝

＝2

9．已知a，b，a+b成等差数列，a，b，ab成等比数列，点P(x，y)为椭圆+＝1上的一点，则x²+xy+y²的最大值为________．

解析：依题意得，解得a＝2，b＝4，得椭圆方程为+＝1，

设P(cosθ，2sinθ)(θ为参数)，则有

x²+xy+y²＝(cosθ)²+×cosθ×2sinθ+4sin²θ

＝2+2sin²θ+sin2θ＝3+sin2θ－cos2θ

＝3+sin(2θ－)≤3+，

故最大值为3+.

答案：3+

8．已知动圆方程x²+y²－xsin2θ+2ysin(θ+)＝0(θ为参数)，那么圆心的轨迹方程是___________．

解析：圆心轨迹的参数方程为：

即

消去参数θ得y²＝1+2x(－≤x≤)．

答案：y²＝1+2x　x∈[－，]

7．在平面直角坐标系xOy中，直线l的参数方程为(参数t∈R)，圆C的参数方程为(参数θ∈[0,2π])，则圆C的圆心坐标为________，圆心到直线l的距离为________．

解析：直线和圆的方程分别是：x+y－6＝0，x²+(y－2)²＝2²，所以圆心坐标为(0,2)，其到直线距离为d＝＝2.

答案：(0,2)　2

6．若P(2，－1)为圆(θ为参数且0≤θ<2π)的弦的中点，则该弦所在的直线方程为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A．x+y+3＝0　 　　　　　B．x+y－3＝0

C．x－y－3＝0　 　　　　　D．x－y+3＝0

解析：∵圆

消去θ，得(x－1)²+y²＝25，

∴圆心C(1,0)，∴k_CP＝－1.

∴弦所在的直线的斜率为1.

∴弦所在的直线方程为y－(－1)＝1·(x－2)，

即为x－y－3＝0.

答案：C

5．点P(x，y)是椭圆2x²+3y²＝12上的一个动点，则x+2y的最大值为　　　　　　　 (　)

A.　 　　　　　B.　　　　　　 C.　 　　　　　　D．2

解析：椭圆+＝1，设点P(cosθ，2sinθ)，

则x+2y＝cosθ+4sinθ＝sin(θ+φ)≤.

答案：B

4．设直线参数方程为(t为参数)，则它的斜截式方程为　　　　　　　 (　)

　A．y＝x+(2－3)　 　　　　　B．y＝x+(3－2)

C．y＝x+(2－3)　 　　　　　D．y＝x+(3－2)

解析：设直线的斜率为，当t＝－4时，x＝0，y＝3－2，故直线的斜截式方程为y＝

x+( 3－2)．

答案：B

3．已知点P(x，y)在曲线(θ为参数)上，则的取值范围为　　　　　 (　)

A．(－，]　 　　　　B．[－，]　　　　 C．[－1,1]　 　　　D．[－，]

解析：　曲线(θ为参数)是以(－2,0)为圆心，以1为半径的圆，设＝k，求的取值范围，即求当直线y＝kx与圆有公共点时k的取值范围，如图结合圆的几何性质可得－≤k≤.

答案：B