2.研究反冲运动的目的是找反冲速度的规律，求反冲速度的关键是确定相互作用的物体系统和其中各物体对地的运动状态．

规律方法　 1、人船模型及其应用

[例1]如图所示，长为l、质量为M的小船停在静水中，一个质量为m的人站在船头，若不计水的阻力，当人从船头走到船尾的过程中，船和人对地面的位移各是多少？

解析:当人从船头走到船尾的过程中,人和船组成的系统在水平方向上不受力的作用,故系统水平方向动量守恒,设某时刻人对地的速度为v₂,船对地的速度为v_1,则mv₂－Mv₁=0,即v₂/v₁=M/m.

在人从船头走到船尾的过程中每一时刻系统的动量均守恒,故mv₂t－Mv₁t=0,即ms₂－Ms₁=0,而s₁+s₂=L

所以

　思考：(1)人的位移为什么不是船长？

　　 (2)若开始时人船一起以某一速度匀速运动，则还满足s₂/s₁=M/m吗？

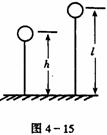[例2]载人气球原静止于高h的高空，气球质量为M，人的质量为m．若人沿绳梯滑至地面，则绳梯至少为多长？

解析：气球和人原静止于空中，说明系统所受合力为零，故人下滑过程中系统动量守恒，人着地时，绳梯至少应触及地面，因为人下滑过程中，人和气球任意时刻的动量大小都相等，所以整个过程中系统平均动量守恒．若设绳梯长为l，人沿绳梯滑至地面的时间为 t，由图4-15可看出，气球对地移动的平均速度为(l－h)/t，人对地移动的平均速度为－h/t(以向上为正方向)．由动量守恒定律，有

　　 M(l－h)/t－m h/t=0．解得 l=h．　　 答案：h

说明：(1)当问题符合动量守恒定律的条件，而又仅涉及位移而不涉及速度时，通常可用平均动量求解．

(2)画出反映位移关系的草图，对求解此类题目会有很大的帮助．

(3)解此类的题目，注意速度必须相对同一参照物．

[例3]如图所示，一质量为m_l的半圆槽体A，A槽内外皆光滑，将A置于光滑水平面上，槽半径为R.现有一质量为m₂的光滑小球B由静止沿槽顶滑下，设A和B均为弹性体，且不计空气阻力，求槽体A向一侧滑动的最大距离．

解析:系统在水平方向上动量守恒,当小球运动到糟的最右端时,糟向左运动的最大距离设为s₁,则m₁s₁=m₂s₂,又因为s₁+s₂=2R,所以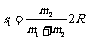

思考：(1)在槽、小球运动的过程中，系统的动量守恒吗？

　　 (2)当小球运动到槽的最右端时，槽是否静止？小球能否运动到最高点？

　　 (3)s₁+S₂为什么等于2R,而不是πR?

[例4]某人在一只静止的小船上练习射击，船、人连同枪(不包括子弹)及靶的总质量为M,枪内有n颗子弹，每颗子弹的质量为m，枪口到靶的距离为L，子弹水平射出枪口相对于地的速度为v₀，在发射后一

发子弹时，前一发子弹已射入靶中，在射完n颗子弹时，小船后退的距离为()

解析:设n颗子弹发射的总时间为t,取n颗子弹为整体,由动量守恒得nmv₀=Mv₁,即nmv₀t=Mv₁t;

设子弹相对于地面移动的距离为s₁,小船后退的距离为s₂,则有: s₁=v₀t, s₂= v₁t;且s₁+s₂=L

解得:.答案C

[例5]如图所示，质量为m、半径为R的小球，放在半径为2R,质量为2m的大空心球内．大球开始静止在光滑的水平面上，当小球从图示位置无初速度地沿大球壁滚到最低点时，大球移动的距离是多少?

解析:设小球相对于地面移动的距离为s₁,大球相对于地面移动的距离为s₂.下落时间为t,则由动量守恒定律得;解得

[例6]如图所示，长20 m的木板AB的一端固定一竖立的木桩，木桩与木板的总质量为10kg，将木板放在动摩擦因数为μ=0. 2的粗糙水平面上，一质量为40kg的人从静止开始以a₁=4 m/s²的加速度从B端向A端跑去，到达A端后在极短时间内抱住木桩(木桩的粗细不计)，求：

(1)人刚到达A端时木板移动的距离．

　(2)人抱住木桩后木板向哪个方向运动，移动的最大距离是多少？(g取10 m/s²)

解析:(1)由于人与木板组成的系统在水平方向上受的合力不为零,故不遵守动量守恒.设人对地的位移为s₁,木板对地的速度为s₂,木板移动的加速度为a₂,人与木板的摩擦力为F,由牛顿定律得:

F=Ma₁=160N;

设人从B端运动到A端所用的时间为t,则s₁=½a₁t, s₂=½a₂t; s₁+s₂=20m

由以上各式解得t=2.0s,s₂=12m

(2)解法一:设人运动到A端时速度为v₁,木板移动的速度为v₂,则v₁=a₁t=8.0m/s, v₂=a₂t=12.0m/s,

由于人抱住木桩的时间极短,在水平方向系统动量守恒,取人的方向为正方向,则Mv₁－mv₂=(M+m)v,得v=4.0m/s.由此断定人抱住木桩后,木板将向左运动.由动能定理得(M+m)μgs=½(M+m)v²解得s=4.0m.

解法二:对木板受力分析,木板受到地面的摩擦力向左,故产生向左的冲量,因此,人抱住木桩后,系统将向左运动.由系统动量定理得(M+m)μgt=(M+m)v,解得v=4.0m/s

由动能定理得(M+m)μgs=½(M+m)v²解得s=4.0m.

1、指在系统内力作用下，系统内一部分物体向某发生动量变化时，系统内其余部分物体向相反方向发生动量变化的现象

2、人船模型的应用条件是：两个物体组成的系统(当有多个物体组成系统时，可以先转化为两个物体组成的系统)动量守恒，系统的合动量为零．

1．若系统在整个过程中任意两时刻的总动量相等，则这一系统在全过程中的平均动量也必定守恒。在此类问题中，凡涉及位移问题时，我们常用“系统平均动量守恒”予以解决。如果系统是由两个物体组成的，合外力为零，且相互作用前均静止。相互作用后运动，则由0=m₁+m₂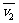得推论0＝m₁s₁+m₂s₂，但使用时要明确s₁、s₂必须是相对地面的位移。

5．解方程。如解出两个答案或带有负号要说明其意义。

[例7]将质量为m；的铅球以大小为v₀、仰角为θ的初速度抛入一个装着砂子的总质量为M的静止砂车中如图所示。砂车与地面间的摩擦力不计，球与砂车的共同速度等于多少？

　　 解析：把铅球和砂车看成一个系统，系统在整个过程中不受水平方向的外力，则水平方向动量守恒．所以：

　　　 m v₀cosθ＝(M+m)v，所以v= m v₀cosθ/(M+m)

答案：m v₀cosθ/(M+m)

说明：某方向合外力为零，该方向动量守恒．

[例8]有N个人，每人的质量均为m，站在质量为M的静止在光滑水平地面上的平板车上，他们从平板车的后端以相对于车身为u的水平速度向后跳下，车就朝前方向运动，求：

　 (1)如果所有的人同时跳下，平板车获得的速度多大？

　 (2)如果一次只跳一个人，平板车获得的速度多大？

解答：他们同时跳下，则nm(u－v)－Mv=0，∴v=u

他们相继跳下，则0=[M+(n－1)m]v₁+m(v₁－u)；

[M+(n－1)m]v₁=[M+(n－2)m]v₂+m(v₂－u)；

[M+(n－2)m]v₂=[M+(n－3)m]v₃+m(v₃－u)；…………

[M+m]v_n-1=Mv_n+m(v_n－u)

∴v₁=mu/(M+nm)；v₂－v₁=mu/[M+(n－1)m]；v₃－v₂=mu/[M+(n－2)m]；……

v_n－vn－₁=mu/[M+m]；

v_n=mu[+++………+]；即v_n＞v

[例9]一玩具车携带若干质量为m的弹丸,车和弹丸的总质量为M,在半径为R的光滑轨道上以速率v₀做匀速圆周运动,若小车每转一周便沿运动方向相对地面以恒定速度u发射一枚弹丸,求:

(1)　　 至少发射多少颗弹丸后,小车开始反向运动?

(2)　　 写出小车反向运动前发射相邻两枚弹丸的时间间隔的表达式.

解析:(1)设发射第一枚弹丸后,玩具车的速度为v₁,由切线方向动量守恒得:

(M－m)v₁+mu=Mv₀　 得

第二枚弹丸发射后,则(M－2m)v₂+mu=(M－m)v₁　 得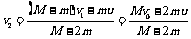

………

则第n枚弹丸发射后,小车的速度为

小车开始反向运动时,v_n≤0,则

(2)发射相邻两枚弹丸的时间间隔就是发射第k(k<n)枚弹丸后小车的周期,即: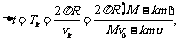

[例10]如图所示，一排人站在沿X轴的水平轨道旁．原点O两侧的人序号都记为n(n＝1、2、3、……)每人只有一个沙袋，X＞0一侧的每个沙袋质量为m＝14 kg， x＜0一侧的每个沙袋质量为 m^/=10 kg．一质量为M=48 kg的小车以某初速度从原点出发向正X方向滑行，不计轨道阻力．当车每经过一人身旁时，此人就把沙袋以水平速度v朝与车速相反的方向沿车面扔到车上，v的大小等手扔袋之前的瞬间车速大小的2n倍(n是此人的序号数)．

　 (1)空车出发后，车上堆积了几个沙袋时车就反向滑行？

　 (2)车上最终有大小沙袋共多少个？

解答：①小车朝正X方向滑行的过程中，第(n－1)个沙袋扔到车上后的车速为v_n－1，第n个沙袋扔到车上后的车速为v_n，由动量守恒[M+(n－1)m] v_n－1－2nm v_n－1=(M+nm)v_n

v_n= v_n－1………①

小车反向运动的条件是v_n－1＞0， v_n＜0，即M－nm＞0，M－(n+1)m＜0，代入数据得

n＜M/m=48/14，n＞M/m－1=34/14，n应为整数，故n=3，即车上堆积3个沙袋后车就反向滑行

②车自反向滑行直到接近x＜一侧第1人所在位置时，车速保持不变，而车的质量为M+3m，若在朝负x方向滑行过程中，第(n-1)个沙袋扔到车上后，车速为v_n-1^/，第n个沙袋扔到车上后车速为v_n^/，现取向左方向为正方向，则由动量守恒得：

[M+3m+(n-1)m^/] v_n-1^/－2nm^/ v_n-1^/=(M+3m+nm^/)v_n^/

v_n^/= v_n-1^/，车不再向左滑行的条件是v_n-1^/＞0，v_n^/＜0，

即(M+3m－nm^/)＞0，(M+3m－(n+1)m^/)≤0

即n＜=9，n≥－1=8，即8≤n＜9，

在n=8时，车停止滑行，故最终有11个沙袋。

试题展示

　　　　　　 专题：人船模型与反冲运动

知识简析　 一、人船模型

4．规定正方向，列方程。

3．分析系统初、末状态各质点的速度，明确系统初、末状态的动量。

2．分析系统所受外力、内力，判定系统动量是否守恒。

1．明确研究对象和力的作用时间，即要明确要对哪个系统，对哪个过程应用动量守恒定律。

(1)动量守恒定律是说系统内部物体间的相互作用只能改变每个物体的动量，而不能改变系统的总动量，在系统运动变化过程中的任一时刻，单个物体的动量可以不同，但系统的总动量相同。

(2)应用此定律时我们应该选择地面或相对地面静止或匀速直线运动的物体做参照物，不能选择相对地面作加速运动的物体为参照物。

(3)动量是矢量，系统的总动量不变是说系统内各个物体的动量的矢量和不变。等号的含义是说等号的两边不但大小相同，而且方向相同。

　 [例2]放在光滑水平面上的A、B两小车中间夹了一压缩的轻质弹簧，用两手分别控制小车处于静止状态，下面说法中正确的是

　 A．两手同时放开后，两车的总动量为零

　 B．先放开右手，后放开左手，而车的总动量向右

　 C．先放开左手，后放开右手，两车的总动量向右

　 D．两手同时放开，同车的总动量守恒；两手放开有先后，两车总动量不守恒

　 解析：根据动量守恒定律的适用条件，两手同时放开，则两车水平方向不受外力作用，总动量守恒；否则，两车总动量不守恒，若后放开左手，则左手对小车有向右的冲量作用，从而两车的总动量向右；反之，则向左．因而，选项ABD正确．

[例3]在质量为M的小车中挂有一单摆，摆球的质量为m₀，小车和单摆以恒定的速度v沿光滑水平地面运动，与位于正对面的质量为m的静止木块发生碰撞，碰撞的时间极短，在此碰撞过程中，下列哪些情况说法是可能发生的(　　　 )

　　 A．小车、木块、摆球的速度都发生变化，分别变为 v_l、v₂、v₃，满足(M+m₀)v=Mv_l十mv₂十m₀v₃

　　 B．摆球的速度不变，小车和木块的速度变化为v_l和v₂，满足Mv=Mv_l十mv₂。

　　 C．摆球的速度不变，小车和木块的速度都变为v_l，满足Mv＝(M+m)v_l

　　 D．小车和摆球的速度都变为v_l，木块的速度变为v₂，满足(M十m₀)v=(M十m₀)v_l十mv₂

分析：小车M与质量为m的静止木块发生碰撞的时间极短，说明在碰撞过程中，悬挂摆球的细线来不及摆开一个明显的角度，因而摆球在水平方向尚未受到力的作用，其水平方向的动量未发生变化，亦即在小车与木块碰撞的过程中，只有小车与木块在水平方向发生相互作用。

解析：在小车M和本块发生碰撞的瞬间，摆球并没有直接与木块发生力的作用，它与小车一起以共同速度V匀速运动时，摆线沿竖直方向，摆线对球的效力和球的重力都与速度方向垂直，因而摆球未受到水平力作用，球的速度不变，可以判定A、D项错误，小车和木块碰撞过程，水平方向无外力作用，系统动量守恒，而题目对碰撞后，小车与木块是否分开或连在一起，没有加以说明，所以两种情况都可能发生，即B、C选项正确。

[例4]如图所示，在光滑水平面上有A、B两小球沿同一条直线向右运动，并发生对心碰撞．设向右为正方向，碰前A、B两球动量分别是p_A＝10kgm/s，p_B=15 kgm/s，碰后动量变化可能是(　　 )

　　 A．Δp_A＝5 kg·m／s　　 Δp_B＝5 kg·m／s

　　 B．Δp_A =－5 kg·m／s　　 Δp_B ＝ 5 kg·m／s

　　 C．Δp_A =5 kg·m／s　　 Δp_B=－5 kg·in／s·

　　 D．Δp_A ＝－20kg·m／s　 Δp_B＝20 kg·m／s

　　　 解析：A．此结果动量不守恒；B．可能；C．B的动量不可能减少，因为是A碰B；D．要出现Δp_A ＝－20kg·m／s只有B不动或向左运动才有可能出现这个结果．答案：B

规律方法　　 1、动量守恒定律的“四性”

在应用动量守恒定律处理问题时,要注意“四性”

①矢量性：动量守恒定律是一个矢量式，，对于一维的运动情况，应选取统一的正方向，凡与正方向相同的动量为正，相反的为负。若方向未知可设与正方向相同而列方程，由解得的结果的正负判定未知量的方向。

②瞬时性：动量是一个状态量，即瞬时值，动量守恒指的是系统任一瞬时的动量恒定，列方程m₁v_l+m₂v₂＝m₁v^/_l+m₂v^/₂时，等号左侧是作用前各物体的动量和，等号右边是作用后各物体的动量和，不同时刻的动量不能相加。

③相对性：由于动量大小与参照系的选取有关，应用动量守恒定律时，应注意各物体的速度必须是相对于同一惯性参照系的速度，一般以地球为参照系

④普适性：动量守恒定律不仅适用于两个物体所组成的系统，也适用于多个物体组成的系统，不仅适用于宏观物体组成的系统，也适用于微观粒子组成的系统。

[例5]一辆质量为60kg的小车上有一质量为40kg的人(相对车静止)一起以2m／s的速度向前运动，突然人相对车以 4m／s的速度向车后跳出去，则车速为多大？

下面是几个学生的解答，请指出错在何处．

(1)解析；人跳出车后，车的动量为60v，人的动量为40(4十v)由动量守恒定律： (60+40)×2＝60v－ 40(4+v)解得： v＝ 0．4 m/s　　　　　　　 　(没有注意矢量性)

(2)解析：选车的方向为正，人跳出车后，车的动量为60v，人的动量一40×4，由动量守恒定律：

　　 (60+40)×2＝60v -40×4，解得v＝6m／s　　　　　　　 　(没有注意相对性)

(3)解析：选车的方向为正，人跳出车后的动量为60v，人的动量一40×(4一2)由动量守恒定律得

(60+40)×2＝60v -40×(4一2)解得v=14/3m/s　　　　　　　　 (没有注意瞬时性)

(4)解析：选地为参照物，小车运动方向为正，据动量守恒定律，(60+40)×2＝60v -40(4-v)解得　　 v=3．6m/s此法正确．

　　 答案：3．6 m／s

[例6]2002年，美国《科学》杂志评出的《2001　 年世界十大科技突破》中，有一项是加拿大萨德伯里　 中微子观测站的成果．该站揭示了中微子失踪的原因，即观测到的中微子数目比理论值少是因为部分中微子在运动过程中转化为一个μ子和一个τ子．　 在上述研究中有以下说法：①该研究过程中牛顿第二定律依然适用；②该研究中能的转化和守恒定律依然适用；③若发现μ子和中微子的运动方向一致，则τ子的运动方向与中微子的运动方向也可能一致；④若发现μ子和中微子的运动方向相反，则τ子的运动方向与中微子的运动方向也可能相反．其中正确的是：

A.①②， B.①③， C.②③， D. ③④；

解析:牛顿运动定律适用于“低速”“宏观”物体,而动量守恒定律和能量守恒定律是自然界中的普适规律,在中微子转化为μ子和τ子时,动量守恒和能量守恒定律仍然适用,当μ子与中微子的运动方向一致时,τ子的运动方向有可能与中微子的运动方向相同,也有可能与中微子运动方向相反;但μ子运动方向与中微子运动方向相反时,τ子的运动方向与中微子的运动方向一定相同.答案C正确.

2、应用动量守恒定律的基本思路