
6.一般的随机事件的概率及其分布列
例13.(2008北京理18) 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
分析:首先要把图形语言转化为文字语言,变为已知条件,转化信息,他们参加活动次数恰好相等会分三种情况,即都参加1项,2项或3项公益活动,分别计算合并,(III)中注意随机变量 的含义为表示这两人参加活动次数之差的绝对值,列出所有可能情况求出。
的含义为表示这两人参加活动次数之差的绝对值,列出所有可能情况求出。
解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40.
(I)该合唱团学生参加活动的人均次数为 .
.
(II)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为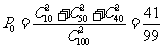 .
.
(III)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件 ,“这两人中一人参加2次活动,另一人参加3次活动”为事件
,“这两人中一人参加2次活动,另一人参加3次活动”为事件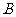 ,“这两人中一人参加1次活动,另一人参加3次活动”为事件
,“这两人中一人参加1次活动,另一人参加3次活动”为事件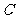 .易知
.易知
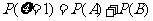
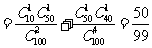 ;
;

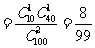 ;
;
 的分布列:
的分布列:
 |
0 |
1 |
2 |
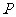 |
 |
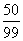 |
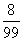 |
 的数学期望:
的数学期望: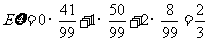 .
.
评注:解决本题的关键是要读懂题意,注意图形语言的转化和题目所要求的要解决的问题。
例14.(2008重庆卷,理18)甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为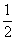 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(Ⅰ) 打满3局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数 的分别列与期望E
的分别列与期望E .
.
分析:打满3局比赛还未停止,说明三人中没有连续获胜的,即第一局如果甲获胜,则第二局丙获胜,第三局乙获胜,对应一种情况;同理,第一局如果乙获胜也对应一种情况。比赛停止时已打局数 最少两局,最多六局,可以分别按前面的做法交叉进行下去,一一计算。
最少两局,最多六局,可以分别按前面的做法交叉进行下去,一一计算。
解:令 分别表示甲、乙、丙在第k局中获胜.
分别表示甲、乙、丙在第k局中获胜.
(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比
赛还未停止的概率为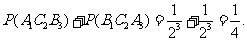
(Ⅱ)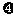 的所有可能值为2,3,4,5,6,且
的所有可能值为2,3,4,5,6,且


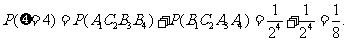

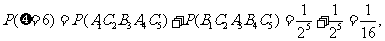
故有分布列
 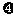 |
2 |
3 |
4 |
5 |
6 |
|
P |
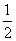 |
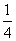 |
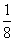 |
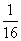 |
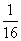 |
从而 (局).
(局).
评注:本题中的随机事件的概率,只能分别按实际情况分类计算。
5.超几何分布
例12.(2008全国II理18)从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.
(1)求从该批产品中任取1件是二等品的概率 ;
;
(2)若该批产品共100件,从中任意抽取2件, 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求 的分布列.
的分布列.
分析:本题已知“取出的2件产品中至多有1件是二等品”的概率,求从该批产品中任取1件是二等品的概率 ,可以用
,可以用 表示出至多有1件是二等品的概率,分两种情况,取出的2件产品中无二等品,和取出的2件产品中恰有1件二等品,利用互斥事件的概率公式求出。(2)中
表示出至多有1件是二等品的概率,分两种情况,取出的2件产品中无二等品,和取出的2件产品中恰有1件二等品,利用互斥事件的概率公式求出。(2)中 的所有取值列出,总体中有特殊,所以是超几何分布类型,按照要求取出求出分布列。
的所有取值列出,总体中有特殊,所以是超几何分布类型,按照要求取出求出分布列。
解:(1)记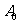 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,  表示事件“取出的2件产品中恰有1件二等品”. 则
表示事件“取出的2件产品中恰有1件二等品”. 则 互斥,且
互斥,且 ,故
,故 
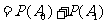

 , 于是
, 于是 .
.
解得 (舍去).
(舍去).
(2) 的可能取值为
的可能取值为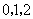 .
.
 若该批产品共100件,由(1)知其二等品有
若该批产品共100件,由(1)知其二等品有 件,故
件,故
 .
.  .
. .
.
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
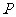 |
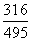 |
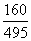 |
 |
评注:本题为超几何分布,是总体中有特殊,能否取到特殊元素,取几个等问题按个数求的分布列,其实质就是按要求取元素的过程。
4.两点分布、二项分布、重复独立试验的概率
例9.(2008安徽卷,理19)为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。某人一次种植了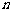 株沙柳,各株沙柳成活与否是相互独立的,成活率为
株沙柳,各株沙柳成活与否是相互独立的,成活率为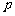 ,设
,设 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望 ,标准差
,标准差 为
为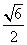 。
。
(Ⅰ)求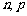 的值并写出
的值并写出 的分布列;
的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率
分析:一株沙柳要么成活,要么不成活,属于两点分布,对于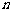 株沙柳来说就是二项分布,可用公式直接表示数学期望和标准差,求出
株沙柳来说就是二项分布,可用公式直接表示数学期望和标准差,求出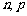 的值并写出
的值并写出 的分布列,3株或3株以上的沙柳未成活,则需要补种,可以从正面解答,也可从反面解答,转化为不需要补种的问题。
的分布列,3株或3株以上的沙柳未成活,则需要补种,可以从正面解答,也可从反面解答,转化为不需要补种的问题。
解:(1)由 得
得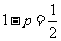 ,
,
从而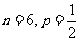 ,
, 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
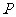 |
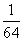 |
 |
 |
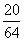 |
 |
 |
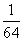 |
(2)记”需要补种沙柳”为事件A,
则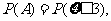 得
得
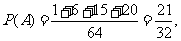 或
或 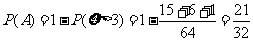
评注:本题为比较简单的二项分布问题,直接运用公式进行计算即可。要对二项分布列必须熟悉。
例10.(08山东卷,理18)甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者对本队赢得一分,答错得零分.假设甲队中每人答对的概率均为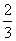 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,且各人回答正确与否相互之间没有影响.用
,且各人回答正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分.
(Ⅰ)求随机变量 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)用 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用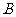 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求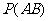 .
.
分析:甲队中每人答对的概率均为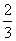 ,
, 表示甲队的总得分,则随机变量
表示甲队的总得分,则随机变量 服从二项分布,乙队中3人答对的概率都不同,各人回答正确与否相互之间没有影响,事件
服从二项分布,乙队中3人答对的概率都不同,各人回答正确与否相互之间没有影响,事件 为相互独立事件,事件
为相互独立事件,事件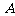 是甲、乙两个队总得分之和等于3,事件
是甲、乙两个队总得分之和等于3,事件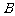 是甲队总得分大于乙队总得分,则
是甲队总得分大于乙队总得分,则 就是甲、乙两个队总得分之和等于3且甲队总得分大于乙队总得分的事件,所以甲、乙两队的分数之间有联系,可以先确定一个,再确定另一个,从而分类求得。
就是甲、乙两个队总得分之和等于3且甲队总得分大于乙队总得分的事件,所以甲、乙两队的分数之间有联系,可以先确定一个,再确定另一个,从而分类求得。
(Ⅰ)解法一:由题意知, 的可能取值为0,1,2,3,且
的可能取值为0,1,2,3,且
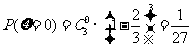 ,
, ,
,
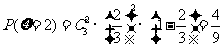 ,
,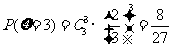 .
.
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
 |
 |
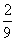 |
 |
 |
 的数学期望为
的数学期望为 .
.
解法二:根据题设可知,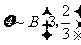 ,
,
因此 的分布列为
的分布列为 ,
, .
.
因为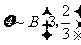 ,所以
,所以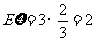 .
.
(Ⅱ)解法一:用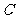 表示“甲得2分乙得1分”这一事件,用
表示“甲得2分乙得1分”这一事件,用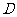 表示“甲得3分乙得0分”这一事件,所以
表示“甲得3分乙得0分”这一事件,所以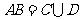 ,且
,且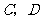 互斥,又
互斥,又

 ,
,
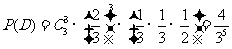 ,
,
由互斥事件的概率公式得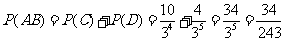 .
.
解法二:用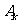 表示“甲队得
表示“甲队得 分”这一事件,用
分”这一事件,用 表示“乙队得
表示“乙队得 分”这一事件,
分”这一事件, .
.
由于事件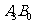 ,
, 为互斥事件,故有
为互斥事件,故有 .
.
由题设可知,事件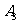 与
与 独立,事件
独立,事件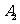 与
与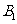 独立,因此
独立,因此
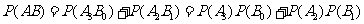
 .
.
评注:本题中涉及到两个队,情况比较复杂,要学会透过现象看本质,仔细分析题目,由浅入深,排除干扰,抓住问题的实质解答问题。另外还要看到两队之间的联系,从而找到解决问题的策略。分类讨论做到不重不漏。
例11.(2008全国二,理18)购买某种保险,每个投保人每年度向保险公司交纳保费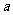 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为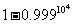 .
.
(Ⅰ)求一投保人在一年度内出险的概率 ;
;
(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50 000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元).
分析:由一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立,可知这些保险是服从二项分布的;保险公司开办该项险种业务除赔偿金外的成本为50 000元,盈利就是该险种总收入减去成本和赔偿金总额,而赔偿金总额与出险的人数为 有关由(Ⅰ)知
有关由(Ⅰ)知 服从二项分布,从而计算出盈利的期望。
服从二项分布,从而计算出盈利的期望。
解:各投保人是否出险互相独立,且出险的概率都是 ,记投保的10 000人中出险的人数为
,记投保的10 000人中出险的人数为 ,则
,则 .
.
(Ⅰ)记 表示事件:保险公司为该险种至少支付10 000元赔偿金,则
表示事件:保险公司为该险种至少支付10 000元赔偿金,则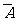 发生当且仅当
发生当且仅当 ,
, 
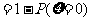
 ,
,
又 ,故
,故 .
.
(Ⅱ)该险种总收入为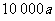 元,支出是赔偿金总额与成本的和.
元,支出是赔偿金总额与成本的和.
支出
 ,
,
盈利
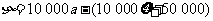 ,
,
盈利的期望为 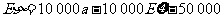 ,
,
由 知,
知,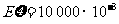 ,
,
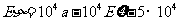
 .
.

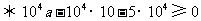
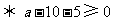
 (元).
(元).
故每位投保人应交纳的最低保费为15元.
评注:本题中的数学环境是以保险为背景考查二项分布列,对于学生来说有些陌生,不易理解,而第二问又是间接地解答问题,所以本题难度较大。
3.互斥事件与相互独立事件的概率
例6.(2008四川卷,理18) 设进入某商场的每一位顾客购买甲种商品的概率为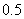 ,购买乙种商品的概率为
,购买乙种商品的概率为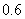 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望。
的分布列及期望。
分析:购买甲、乙两种商品是相互独立的,1位顾客购买甲、乙两种商品中的一种有两种情况,买甲不买乙或买乙不买甲,又是互斥事件,按互斥事件的概率进行计算;进入商场的1位顾客至少购买甲、乙两种商品中的一种,对于至少问题,可以正面计算,也可以反面计算;进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数可以为0,1,2,3,应该是(Ⅱ)的二项分布
解:记 表示事件:进入商场的1位顾客购买甲种商品,
表示事件:进入商场的1位顾客购买甲种商品,
记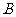 表示事件:进入商场的1位顾客购买乙种商品,
表示事件:进入商场的1位顾客购买乙种商品,
记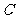 表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
记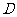 表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
(Ⅰ) ,
, 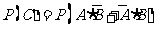


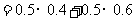
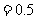
(Ⅱ) ,
,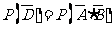


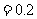
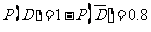
(Ⅲ)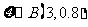 ,故
,故 的分布列
的分布列 ,
,
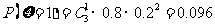 ,
,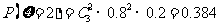
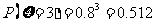 , 所以
, 所以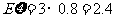
评注:此题重点考察相互独立事件的概率计算,以及求随机变量的概率分布列和数学期望;
分清相互独立事件的概率求法,对于“至少”常从反面入手常可起到简化的作用。
例7.(2008天津卷,文18)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为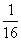 .
.
(Ⅰ)求乙投球的命中率 ;
;
(Ⅱ)求甲投球2次,至少命中1次的概率;
(Ⅲ)若甲、乙两人各投球2次,求两人共命中2次的概率.
分析:乙投球2次均未命中的概率为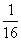 ,求乙投球的命中率
,求乙投球的命中率 ,属于逆向思维,列出方程解出即可。甲投球2次,至少命中1次,对于“至少”问题可以正面解答,也可以反面解答。甲、乙两人各投球2次,求两人共命中2次,应该有多种情况,分类计算。
,属于逆向思维,列出方程解出即可。甲投球2次,至少命中1次,对于“至少”问题可以正面解答,也可以反面解答。甲、乙两人各投球2次,求两人共命中2次,应该有多种情况,分类计算。
(Ⅰ)解法一:设“甲投球一次命中”为事件A,“乙投球一次命中”为事件B.
由题意得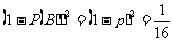
解得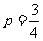 或
或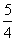 (舍去),所以乙投球的命中率为
(舍去),所以乙投球的命中率为 .
.
解法二:设设“甲投球一次命中”为事件A,“乙投球一次命中”为事件B.
由题意得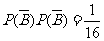 ,于是
,于是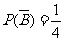 或
或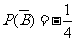 (舍去),故
(舍去),故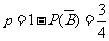 .
.
所以乙投球的命中率为 .
.
(Ⅱ)解法一:由题设和(Ⅰ)知 .
.
故甲投球2次至少命中1次的概率为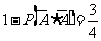
解法二:由题设和(Ⅰ)知
故甲投球2次至少命中1次的概率为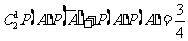
(Ⅲ)由题设和(Ⅰ)知,
甲、乙两人各投球2次,共命中2次有三种情况:甲、乙两人各中一次;甲中两次,乙两次均不中;甲两次均不中,乙中2次。概率分别为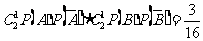 ,
,
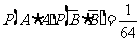 ,
,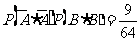
所以甲、乙两人各投两次,共命中2次的概率为 .
.
评注:本小题是概率部分的常规题目,主要考查随机事件、互斥事件、相互独立事件等概率的基础知识,考查运用概率知识解决实际问题的能力,分类要做到不重不漏。
例8.(江苏省盐城中学2008)某城市有甲、乙、丙、丁4个旅游景点,一位客人游览这4个景点的概率都是0.6,且客人是否游览哪个景点互不影响.设 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求 的分布列及数学期望;
的分布列及数学期望;
 (Ⅱ) 记“函数
(Ⅱ) 记“函数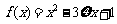 在区间
在区间 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
分析:“客人游览甲景点”、“客人游览乙景点”、“客人游览丙景点” 、“客人游览丁景点” 是相互独立的,按相互独立事件的概率计算,列出分布列,求出数学期望。“函数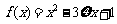 在区间
在区间 上单调递增”,可以得到二次函数的对称轴与区间的位置关系,从而得到
上单调递增”,可以得到二次函数的对称轴与区间的位置关系,从而得到 的范围。
的范围。
解:(1)分别设“客人游览甲景点”、“客人游览乙景点”、“客人游览丙景点” 、
“客人游览丁景点”为事件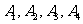 ,由已知
,由已知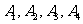 相互独立,
相互独立,
且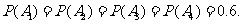
客人游览的景点数的可能取值为0,1,2,3,4;相应的,客人没有游览的景点数的可能取值为4,3,2,1,0.所以 的可能取值为0,2, 4
的可能取值为0,2, 4
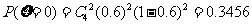
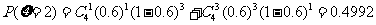
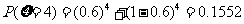
所以 的分布列为
的分布列为
 |
0 |
2 |
4 |
|
P |
0.3456 |
0.4992 |
0.1552 |

(2)因为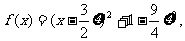 所以函数
所以函数 在区间
在区间 上单调递增.要使
上单调递增.要使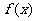 在
在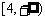 上单调递增,当且仅当
上单调递增,当且仅当 即
即
从而
评注:本题是相互独立事件的概率的求法,注意随机变量 的取值要一一列出,并求出各种情况的概率,列出分布列。另外本题还与函数相结合计算概率。
的取值要一一列出,并求出各种情况的概率,列出分布列。另外本题还与函数相结合计算概率。
2.几何概型
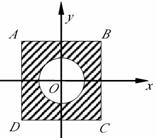 例3.(2008江苏卷,6)在平面直角坐标系
例3.(2008江苏卷,6)在平面直角坐标系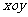 中,设
中,设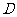 是横坐标与纵坐标的绝对值均不大于2的点构成的区域,
是横坐标与纵坐标的绝对值均不大于2的点构成的区域,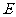 是到原点的距离不大于1的点构成的区域,向
是到原点的距离不大于1的点构成的区域,向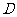 中随机投一点,则所投点在
中随机投一点,则所投点在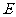 中的概率是
中的概率是
分析:本小题考查古典概型,其概率应为几何图形的面积比。
如图:区域D 表示边长为4 的正方形的内部(含边界),区域E 表示单位圆及其内部,因此.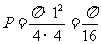
答案: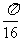
评注:在解决几何概型问题时,要弄清整个事件的区域长度(面积或体积),以及所研究事件的区域长度(面积或体积),特别是平面几何图形的构成常常是考查的焦点,有可能与定积分相联系。
例4.(2008宁夏银川一中)如图所示,墙上挂有一边长为 的正方形木板,它的四个角的空白部分都是以正
的正方形木板,它的四个角的空白部分都是以正
 方形的顶点为圆心,半径为
方形的顶点为圆心,半径为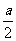 的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,
的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,
则他击中阴影部分的概率是 ( )
A. B.
B. C.
C.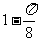 D.与
D.与 的取值有关
的取值有关
分析:本小题考查古典概型,其概率应为几何图形的面积比。其中阴影部分的面积要通过规则的图形的面积求出,即正方形的面积去掉一个圆的面积。
解:正方形的面积为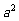 ,而四个角空白部分合起来为半径为
,而四个角空白部分合起来为半径为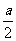 的一个圆,面积为
的一个圆,面积为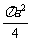 ,所以他击中阴影部分的概率是
,所以他击中阴影部分的概率是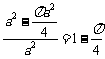 ,故选A。
,故选A。
答案:A
评注:在解决几何概型问题时,对于不规则图形的面积要通过求定积分或规则图形的面积求出。
例5.(2007宁夏卷,文20)设有关于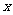 的一元二次方程
的一元二次方程 .
.
(Ⅰ)若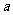 是从
是从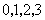 四个数中任取的一个数,
四个数中任取的一个数,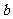 是从
是从 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若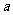 是从区间
是从区间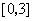 任取的一个数,
任取的一个数,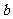 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
分析:一元二次方程有实根的条件为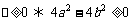 ,即
,即 。题(Ⅰ)可用列举法列出所有的基本事件,找出符合条件
。题(Ⅰ)可用列举法列出所有的基本事件,找出符合条件 的基本事件。题(Ⅱ)就是几何概型。可作出试验的总区域,和符合条件的区域,应该是把
的基本事件。题(Ⅱ)就是几何概型。可作出试验的总区域,和符合条件的区域,应该是把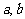 看作有序数对
看作有序数对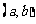 对于平面上的点,可画出平面区域解答。
对于平面上的点,可画出平面区域解答。
解:设事件 为“方程
为“方程 有实根”.
有实根”.
当 ,
,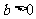 时,方程
时,方程 有实根的充要条件为
有实根的充要条件为 .
.
(Ⅰ)基本事件共12个:
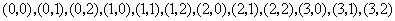 .其中第一个数表示
.其中第一个数表示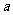 的取值,第二个数表示
的取值,第二个数表示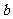 的取值.
的取值.
 事件
事件 中包含9个基本事件,事件
中包含9个基本事件,事件 发生的概率为
发生的概率为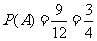 .
.
(Ⅱ)试验的全部结束所构成的区域为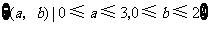 .
.
构成事件 的区域为
的区域为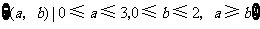 .
.
所以所求的概率为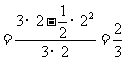 .
.
评注:本题容纳了古典概型和几何概型的解法,要善于区分提炼,并进行转化,把数组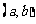 看成平面内的点即可转化为平面区域问题用面积解答。
看成平面内的点即可转化为平面区域问题用面积解答。
1.古典概型
例1.(2008海南卷,文19)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:5,6,7,8,9,10.
把这6名学生的得分看成一个总体.
(Ⅰ)求该总体的平均数;
(Ⅱ)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
分析:本题为古典概型,先计算出总体平均数,列出所有的抽取情况,再从中找出符合条件的即两人的得分平均数与总体平均数之差的绝对值不超过0.5的所有情况。
解:(Ⅰ)总体平均数为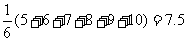
(Ⅱ)设 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
从总体中抽取2个个体全部可能的基本结果有: ,
, ,
, ,
,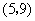 ,
,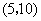 ,
,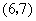 ,
,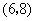 ,
,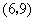 ,
, ,
,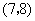 ,
,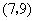 ,
, ,
, ,
, ,
,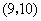 .共15个基本结果.事件
.共15个基本结果.事件 包括的基本结果有:
包括的基本结果有: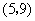 ,
,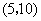 ,
,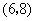 ,
,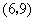 ,
, ,
,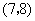 ,
,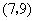 .共有7个基本结果.所以所求的概率为
.共有7个基本结果.所以所求的概率为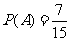 .
.
评注:文科关于概率大题的考查基本上列举法,即列出所有的基本事件,从中找出满足要求的基本事件,然后求出它们的个数比即可。
例2.(2008山东淄博,理)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: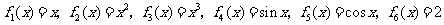 .
.
(Ⅰ)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.
分析:本题中每一张卡片被抽取到是等可能的,可利用排列组合的知识随机抽取和按要求无放回的抽取,从而计算出每个事件的概率,列出分布列求出数学期望。
解:(Ⅰ)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知 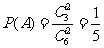 .
.
(Ⅱ)ξ可取1,2,3,4


故ξ的分布列为
|
ξ |
1 |
2 |
3 |
4 |
|
P |
 |
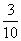 |
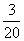 |
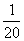 |
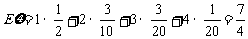
答:ξ的数学期望为 .
.
评注:在解答本题时,要弄清随机变量 的所有取值情况,题目中有三个奇函数,三个偶函数,所以最多取4次就一定能取到记有偶函数的卡片,从而停止抽取。注意不放回地抽取,上一次的抽取结果会影响下一次的抽取,即下一次的总体个数减少。
的所有取值情况,题目中有三个奇函数,三个偶函数,所以最多取4次就一定能取到记有偶函数的卡片,从而停止抽取。注意不放回地抽取,上一次的抽取结果会影响下一次的抽取,即下一次的总体个数减少。
19.(08四川延考)已知 ,
,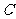 为空间中一点,且
为空间中一点,且 ,则直线
,则直线 与平面
与平面
所成角的正弦值为 。
 [答案]:由对称性点
[答案]:由对称性点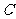 在平面
在平面 内的射影
内的射影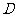 必在
必在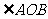 的平分线上作
的平分线上作 于
于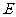 ,连结
,连结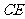 则由三垂线定理
则由三垂线定理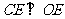 ,
,
设
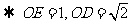 ,又
,又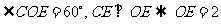 ,所以
,所以 ,因此直线
,因此直线 与平面
与平面 所成角的正弦值
所成角的正弦值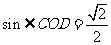
20(08湖南理)
.对有n(n≥4)个元素的总体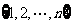 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体
 和
和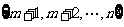 (m是给定的正整数,且2≤m≤n-2),再从
(m是给定的正整数,且2≤m≤n-2),再从
每个子总体中各随机抽取2个元素组成样本.用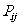 表示元素i和j同时出现在样
表示元素i和j同时出现在样
本中的概率,则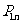 =
; 所有
=
; 所有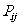 (1≤i<j≤
(1≤i<j≤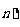 的和等于
.
的和等于
.
[答案]: 第二空可分:
第二空可分:
①当  时,
时, 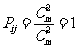 ;
;
②当 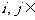
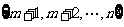 时,
时, 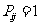 ;
;
③当

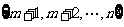 时,
时, 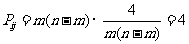 ;
;
所以

18.(08四川延考)已知函数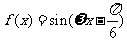
 在
在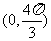 单调增加,在
单调增加,在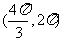 单调减少,则
单调减少,则 。
。
[答案]:由题意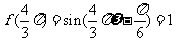
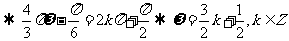
又 ,令
,令 得
得 。(如
。(如 ,则
,则 ,
,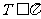 与已知矛盾)
与已知矛盾)
17.(08四川延考)设等差数列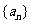 的前
的前 项和为
项和为 ,且
,且 。若
。若 ,则
,则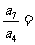 。
。
[答案]: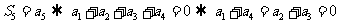 ,取特殊值
,取特殊值
令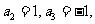
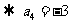
 ,所以
,所以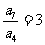
16.(08四川延考)函数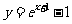
 的反函数为 。
的反函数为 。
[答案]: ,所以反函数
,所以反函数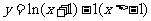 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com