
5.某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是 ( D )
A.10% B.15% C.18% D.20%
4.(2009江西)函数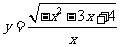 的定义域为 ( D )
的定义域为 ( D )
A.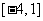 B.
B. C.
C.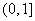 D.
D.
3.(2004湖北)已知f( )=
)=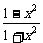 ,则f(x)的解析式可取为( )
,则f(x)的解析式可取为( )
A.  B.
B.  C.
C. 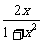 D.
D. 
2. 已知函数 的定义域是
的定义域是 ,则实数a的取值范围是 ( B
)
,则实数a的取值范围是 ( B
)
A.a> B.
B.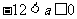 C.
C.  D.
D.
1.(2006湖北)设 ,则
,则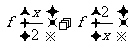 的定义域为
( B )
的定义域为
( B )
A.  B.
B.

C. 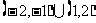 D.
D. 
1.题型的结构与解答特点:
11.预测题
(1).(2008广东)已知两不等的实数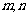 满足
满足
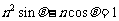 则过点
则过点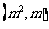 和
和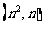 的直线与单位圆的位置关系为(
)
的直线与单位圆的位置关系为(
)
A.相切 B.相离 C.相交 D.不确定
分析:本题给出的是两个方程,所研究的是直线与圆的位置关系,,需要两点确定的直线方程,通过观察就可以把已知的方程转化为所求直线的方程,从而判断直线与圆的位置关系.
解:因为 实数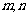 满足
满足
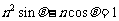 ,所以点
,所以点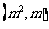 和
和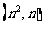 的坐标都适合直线
的坐标都适合直线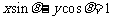 ,即两点确定的直线方程为
,即两点确定的直线方程为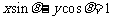 ,原点到此直线的距离为
,原点到此直线的距离为 ,所以直线与圆相切.故选A
,所以直线与圆相切.故选A
答案:A
评注:不要直接由两点式写方程,要注意观察并把已知条件转化,减少计算量.
(2).(08届莆田四中)已知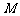 是
是 内一点,且
内一点,且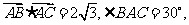 若
若 、
、 、
、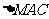 的面积分别为
的面积分别为 、
、 , 则
, 则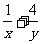 的最小值是( )
的最小值是( )
A.9 B. 16 C. 18 D. 20
分析:已知条件为向量的数量积与夹角,可以得到两边之积,再由两边与夹角求得 的面积,另一方面,
的面积,另一方面,  的面积又为
的面积又为 、
、 、
、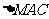 的面积之和
的面积之和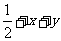 ,从而实现了由向量向代数式的转化.然后用均值不等式求得最值.
,从而实现了由向量向代数式的转化.然后用均值不等式求得最值.
解:∵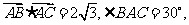 ∴
∴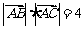 ,∴
,∴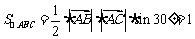 ,又因为
,又因为 的面积为
的面积为 、
、 、
、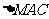 的面积之和
的面积之和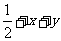 ,∴得
,∴得
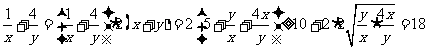 当且仅当
当且仅当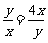 时取等号.故选C.
时取等号.故选C.
答案:C
评注:本题完成了由向量向函数方程之间的转化,进而又转化为用均值不等式求最值.做题时要注意条件的联系性和化归的数学思想.
(3)(宁夏银川一中)
|

 项和是
项和是
|
A.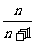 B.
B. C.
C. D.
D.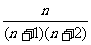
分析:把题目中的函数求出,得到解析式,从而转化为数列的通项与前 项的和.
项的和.
解: 由函数 知
知 ,所以
,所以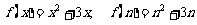 , 所以
, 所以
 ,
, 项和为
项和为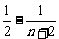 =
= ,故选C.
,故选C.
答案:C
评注:本题中给出的已知
条件是函数与导函数,由导函数确定原函数,从而求得数列的通项公式,然后求出前 项的和.
项的和.
(4)(江苏省盐城中学)求直线 (
( )被曲线
)被曲线 所截的弦长.
所截的弦长.
分析:本题给出的是参数方程和极坐标方程,要求弦长,就要转化为普通方程.
解:将方程 ,
,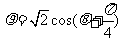 分别化为普通方程:
分别化为普通方程: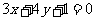 ,
,
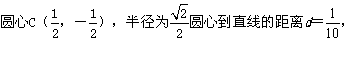
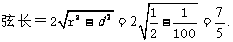
评注:对于参数方程和极坐标方程的方程,可以直接求解,也可以转化为普通方程求解出.
(5).(原创)设函数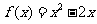 ,若
,若 ,则点
,则点 所形成的区域的面积为 ( )
所形成的区域的面积为 ( )
A.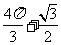 B.
B.  C.
C.  D.
D. 
分析:首先分析由 所确定的平面区域,再根据区域的形状求其面积.
所确定的平面区域,再根据区域的形状求其面积.
解:由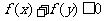 ,得
,得 ,即
,即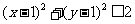 ,所表示的区域为以
,所表示的区域为以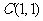 为圆心,以
为圆心,以 为半径的圆面.由
为半径的圆面.由 ,
,
得 ,即
,即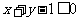 ,所表示的区域为直线
,所表示的区域为直线 的左下方.故点
的左下方.故点 所形成的区域如图阴影部分所示.
所形成的区域如图阴影部分所示.
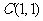 到直线
到直线 的距离为
的距离为 ,又
,又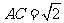 ,故
,故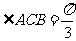 ,
,
 ,对应的圆心角角为
,对应的圆心角角为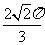 ,扇形ABC的面积为
,扇形ABC的面积为 ;
;
又 的面积为
的面积为 ,故阴影部分的面积为
,故阴影部分的面积为 .即点
.即点 所形成的区域的面积为
所形成的区域的面积为 .选D.
.选D.


评注:考查圆的标准方程,点到直线的距离,一元二次方程表示平面区域,扇形的面积以及函数的表示等知识.考查运算能力和化归思想.函数,不等式的内容都是比较容易与其它知识相结合的知识点,本题在形式上是函数和不等式问题,但剖析之后可以发现,其实质是圆与线性规划相结合的问题.高考中,知识的交汇试题是主流,很多题目都是以一个知识点为载体考查另一个知识点,解题时一定要善于分析,透过表面看透问题的实质,从而合理转化,寻求问题的解决途径.
(6).(原创)已知过点(0,3)的直线 与函数
与函数 的导函数的图象交于
的导函数的图象交于 两点, ,且
两点, ,且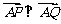 ,其中
,其中
(1)求直线 的方程,并求
的方程,并求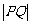 的长.
的长.
(2)问若 ,问实数m取何值时,使得
,问实数m取何值时,使得 的图象恒在
的图象恒在 的图象的上方?
的图象的上方?
分析:根据求导公式,将函数问题转化为抛物线与直线的位置关系问题,通过解方程组,由韦达定理和向量的数量积坐标运算,利用待定系数法求解.
 解: 函数
解: 函数 的导函数为
的导函数为 ,其图象为开口向上的抛物线, 因为直线
,其图象为开口向上的抛物线, 因为直线 过点(0,3), 与抛物线交于
过点(0,3), 与抛物线交于 两点,所以直线
两点,所以直线 的斜率存在,设为
的斜率存在,设为 ,则直线
,则直线 的方程为
的方程为 ,解方程组
,解方程组 消去
消去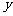 得:
得: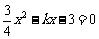 ,△
,△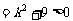 ,方程组有两解,设
,方程组有两解,设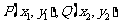 ,则
,则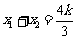 ,
, ,∴
,∴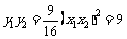 ,
,
∵ ,∴
,∴ ,
,
又∵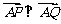 ∴
∴ ,
,
即 ,∴
,∴ ,
,
即 ∴
∴ 或
或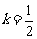 ,
,
①当 时,直线
时,直线 的方程为
的方程为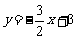 ,
,
此时, ,
,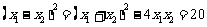 ,
,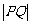 =
=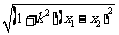 =
= .
.
②当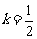 时,直线
时,直线 的方程为
的方程为 ,此时,
,此时, ,
,
 ,
,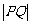 =
=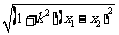 =
= .
.
(2)设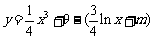 ,定义域为
,定义域为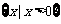
则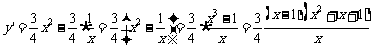 ,令
,令 ,得
,得 ,
,
∴当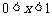 时,
时, ,
,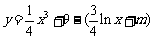 为减函数;
为减函数;
当 时,
时,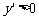 ,
,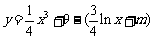 为增函数;∴当
为增函数;∴当 时,
时,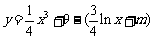 最小,最小值为
最小,最小值为 ,∴要使得
,∴要使得 的图象恒在
的图象恒在 的图象的上方,需使最小值
的图象的上方,需使最小值 >0,即
>0,即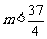
评注:考查函数求导,利用导数求函数的最值, 向量的数量积, 考查直线与圆锥曲线的位置关系等基础知识,考查利用韦达定理计算弦长等综合运算求解能力.本题通过函数求导,把问题转化为研究直线与圆锥曲线的位置关系,并把两曲线的位置关系的讨论转化为利用导数研究函数的最值的综合性题目.做题时要仔细审题,逐步翻译,求解直线或圆锥曲线的方程时往往要先设后求,利用待定系数法和解方程组法由韦达定理解答.在解答问题时要注意直线的斜率是否存在,解方程组时,判别式是否大于0,函数的定义域等这些细节问题.
10.立体问题转化为平面(向量)问题
例17.(2008江苏海头高级中学)如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为2的正方形,P是BC中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为__ _ .
分析:研究最短距离,需要把立体图展为平面图,由两点间的线段最短,求线段的长。
解:把圆柱侧面展开,并把里面也展开,如图所示,则这只蚂蚁取得米粒所需经过的
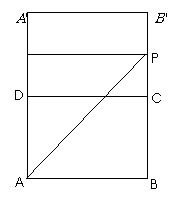
 最短路程为展开图中的线段
最短路程为展开图中的线段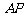 ,则
,则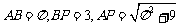
答案:
评注:研究立体问题常常以平面为基准,把立体问题
转化为平面问题,把曲线问题转化为直线问题,
这是解决问题的转化与化归思想。
例18.(2008年安徽卷,理18)如图,在四棱锥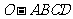 中,
中,
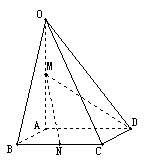 底面
底面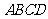 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,
 ,
, 为
为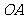 的中点,
的中点, 为
为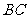 的中点
的中点
(Ⅰ)证明:直线
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
分析:要证线面平行,可以在面内找 的平行线,取
的平行线,取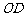 的中点,通过线线平行证出,也可以找平面的平行平面通过面面平行证出; 异面直线AB与MD所成角可以通过平移转化为平面角求出;而(Ⅲ)中点B到平面OCD的距离不易找出,可以利用线
的中点,通过线线平行证出,也可以找平面的平行平面通过面面平行证出; 异面直线AB与MD所成角可以通过平移转化为平面角求出;而(Ⅲ)中点B到平面OCD的距离不易找出,可以利用线 转化为点A到平面OCD的距离求出.还可以用向量法通过计算解答各题.
转化为点A到平面OCD的距离求出.还可以用向量法通过计算解答各题.
 解法一:(综合法) (1)取OB中点E,连接ME,NE
解法一:(综合法) (1)取OB中点E,连接ME,NE

又

(2)
 为异面直线
为异面直线 与
与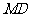 所成的角(或其补角)
所成的角(或其补角)
作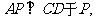 连接
连接

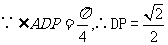
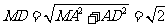
 所以
所以  与
与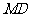 所成角的大小为
所成角的大小为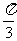
(3)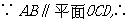 点A和点B到平面OCD的距离相等,连接OP,过点A作
点A和点B到平面OCD的距离相等,连接OP,过点A作
 于点Q,
于点Q,
又  ,线段AQ的长就是点A到平面OCD的距离
,线段AQ的长就是点A到平面OCD的距离
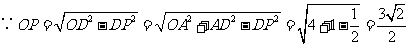 ,
,
 ,所以点B到平面OCD的距离为
,所以点B到平面OCD的距离为
解法二.(向量法)作 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为 轴建立坐标系
轴建立坐标系

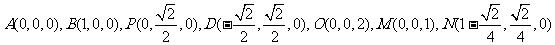 (1)
(1)
设平面OCD的法向量为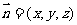 ,则
,则
即
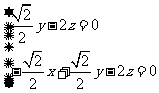 取
取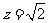 ,解得
,解得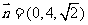
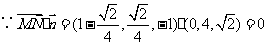

(2)设 与
与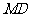 所成的角为
所成的角为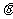 ,
,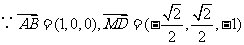
 ,
,  与
与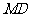 所成角的大小为
所成角的大小为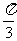
(3)设点B到平面OCD的距离为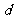 ,则
,则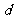 为
为 在向量
在向量 上的投影的绝对值,
上的投影的绝对值,
由  , 得
, 得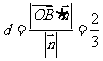 .所以点B到平面OCD的距离为
.所以点B到平面OCD的距离为
评注:立体几何问题一般都可以用两种方法综合法和向量法.都要经过转化,把立体问题转化为平面问题,将空间问题转化为代数运算从而证得求出.
 例19.(2008山东卷,理20)如图,已知四棱锥
例19.(2008山东卷,理20)如图,已知四棱锥 ,底面
,底面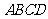 为菱形,
为菱形,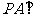 平面
平面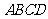 ,
,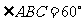 ,
,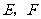 分别是
分别是 的中点.
的中点.
(Ⅰ)证明: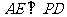 ;
;
(Ⅱ)若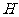 为
为 上的动点,
上的动点, 与平面
与平面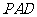 所成
所成
最大角的正切值为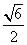 ,求二面角
,求二面角 的余弦值.
的余弦值.
分析: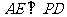 比较容易证出,可以转化为线面垂直证明出, (Ⅱ)的点
比较容易证出,可以转化为线面垂直证明出, (Ⅱ)的点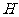 为
为 上的动点,而且
上的动点,而且 与平面
与平面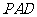 所成最大角不太容易找到,根据(Ⅰ)就要转化为
所成最大角不太容易找到,根据(Ⅰ)就要转化为 点到
点到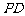 的距离最短,然后求出确定位置.另外,对于点的位置不确定而且比较容易建立直角坐标系时,用坐标计算比较简单。
的距离最短,然后求出确定位置.另外,对于点的位置不确定而且比较容易建立直角坐标系时,用坐标计算比较简单。
解:(Ⅰ)证明:由四边形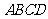 为菱形,
为菱形,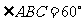 ,可得
,可得 为正三角形.
为正三角形.
因为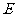 为
为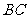 的中点,所以
的中点,所以 .又
.又 ,因此
,因此 .
.
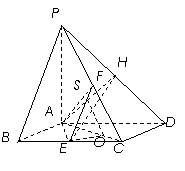 因为
因为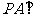 平面
平面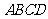 ,
, 平面
平面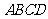 ,所以
,所以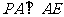 .
.
而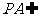 平面
平面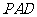 ,
, 平面
平面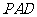 且
且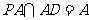 ,
,
所以 平面
平面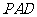 .又
.又 平面
平面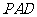 ,所以
,所以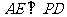 .
.
(Ⅱ)解:设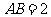 ,
,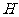 为
为 上任意一点,连接
上任意一点,连接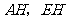 .
.
由(Ⅰ)知 平面
平面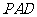 ,则
,则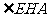 为
为 与平面
与平面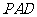 所成的角.
所成的角.
在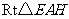 中,
中, ,所以当
,所以当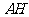 最短时,
最短时,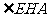 最大,
最大,
即当 时,
时,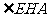 最大.此时
最大.此时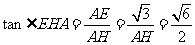 ,
,
因此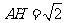 .又
.又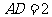 ,所以
,所以 ,所以
,所以 .
.
解法一:因为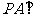 平面
平面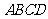 ,
,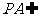 平面
平面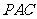 ,所以平面
,所以平面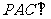 平面
平面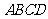 .
.
过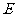 作
作 于
于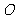 ,则
,则 平面
平面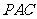 ,过
,过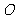 作
作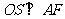 于
于 ,连接
,连接 ,则
,则 为二面角
为二面角 的平面角,在
的平面角,在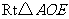 中,
中,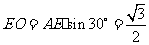 ,
, ,又
,又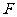 是
是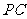 的中点,在
的中点,在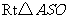 中,
中,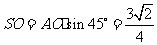 ,
,
又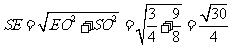 ,在
,在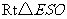 中,
中,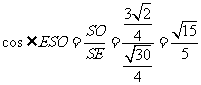 ,即所求二面角的余弦值为
,即所求二面角的余弦值为 .
.
解法二:由(Ⅰ)知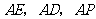 两两垂直,以
两两垂直,以 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又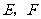 分别为
分别为 的中点,所以
的中点,所以

 ,
,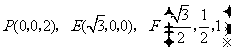 ,所以
,所以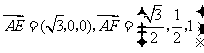 .
.
设平面 的一法向量为
的一法向量为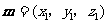 ,
,
则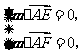 因此
因此
取 ,则
,则 ,因为
,因为 ,
, ,
, ,
,
所以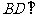 平面
平面 ,故
,故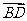 为平面
为平面 的一法向量.又
的一法向量.又 ,
,
所以 .因为二面角
.因为二面角 为锐角,
为锐角,
所以所求二面角的余弦值为 .
.
评注:本题为探索性问题,难度比较大。特别是在使用线面角时不易找出。这就需要我们耐心分析,仔细体会前后问之间的关系,能否打通思路,把问题进行适当地转化,做到立体问题平面化,几何问题代数化,利用化归思想解答问题。
9.平面向量、解析几何中的化归思想
例15.(2008全国Ⅰ,理10)若直线 通过点
通过点 ,则( )
,则( )
A. B.
B.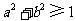 C.
C.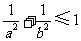 D.
D.
分析:点 是单位圆上的点,,则可以通过直线与单位圆的位置关系来转化。,当然也可以把直线
是单位圆上的点,,则可以通过直线与单位圆的位置关系来转化。,当然也可以把直线 看作等式或看作向量的数量积来解答。
看作等式或看作向量的数量积来解答。
解法一:由题意知直线 与圆
与圆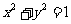 有交点,则
有交点,则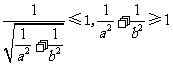 .
.
解法二:设向量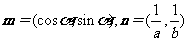 ,由题意知
,由题意知
由 可得
可得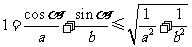
答案: D
评注:本题中的两种方法都是把已知条件进行了转化,利用化归的思想解决问题不适为捷径,方法比较活跃,知识连接成网,这要靠我们平时积累和总结。
例16.(全国Ⅱ,理21)设椭圆中心在坐标原点,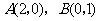 是它的两个顶点,直线
是它的两个顶点,直线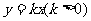 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若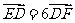 ,求
,求 的值;
的值;
(Ⅱ)求四边形 面积的最大值.
面积的最大值.
分析:本题中涉及到的点比较多,其中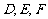 都在直线
都在直线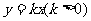 上,(Ⅰ)中的向量要用点的坐标表示出,所以可以先设出各点的坐标,再转化为关于
上,(Ⅰ)中的向量要用点的坐标表示出,所以可以先设出各点的坐标,再转化为关于 的方程解出,(Ⅱ)中的四边形
的方程解出,(Ⅱ)中的四边形 面积可以转化为两个三角形的面积求出,可以都以
面积可以转化为两个三角形的面积求出,可以都以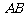 为公共边,也可以以
为公共边,也可以以 为公共边求出。
为公共边求出。
 (Ⅰ)解:依题设得椭圆的方程为
(Ⅰ)解:依题设得椭圆的方程为 ,
,
直线 的方程分别为
的方程分别为 ,
,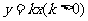 .
.
如图,设 ,其中
,其中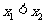 ,
,
且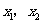 满足方程
满足方程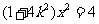 ,故
,故 .①
.①
由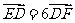 知
知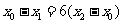 ,得
,得 ;
;
 由
由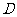 在
在 上知
上知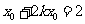 ,得
,得 .所以
.所以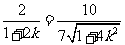 ,
,
化简得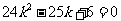 ,解得
,解得 或
或 .
.
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点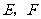 到
到 的距离分别为
的距离分别为 ,
, .
.
 ,所以四边形
,所以四边形 的面积为
的面积为
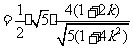


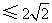 ,
,
当 ,即当
,即当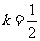 时,上式取等号.所以
时,上式取等号.所以 的最大值为
的最大值为 .
.
解法二:由题设, ,
, .设
.设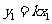 ,
, ,由①得
,由①得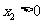 ,
, ,
,
故四边形 的面积为
的面积为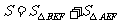
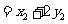


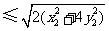
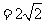 ,
,
当 时,上式取等号.所以
时,上式取等号.所以 的最大值为
的最大值为 .
.
评注:解析几何中的问题常常与向量、函数、方程、不等式等问题相联系,进行转化解答。
8.数列问题的转化
例13.(2009莱阳高三理)若数列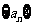 满足
满足 ,则称数列
,则称数列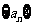 为调和数列。已知数列
为调和数列。已知数列 为调和数列,且
为调和数列,且 ,则
,则 。
。
分析:根据调和数列的定义,可以看出其倒数数列符合等差数列的定义,由此可以转化,利用等差数列的定义求出前 项和。
项和。
解:根据调和数列的定义知:数列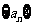 为调和数列,则
为调和数列,则 ,也就是数列
,也就是数列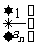 为等差数列,现在数列
为等差数列,现在数列 为调和数列,则数列
为调和数列,则数列 为等差数列,那么由
为等差数列,那么由 ,得
,得 ,
, 20
20
答案:20
评注:本题为新定义题,但也不要被表象所迷惑,通过现象看本质,转化为我们熟悉的特殊数列等差数列进一步解答,此题中注意角色的变化,数列 为调和数列,数列
为调和数列,数列 为等差数列是解题的关键。
为等差数列是解题的关键。
例14.(2008陕西卷,文20)已知数列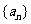 的首项
的首项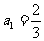 ,
, ,
,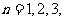 ….
….
(Ⅰ)证明:数列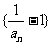 是等比数列;(Ⅱ)数列
是等比数列;(Ⅱ)数列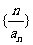 的前
的前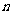 项和
项和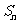 .
.
分析:对于证明数列为等比数列,要按定义证明,但证明完后也提示我们下一步要用等比数列求出数列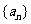 的通项公式,然后进一步判断数列
的通项公式,然后进一步判断数列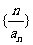 的类型,从而求出其前
的类型,从而求出其前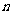 项和
项和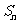 。
。
解:(Ⅰ)
 ,
,
 ,
,

 ,又
,又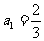 ,
,
 ,
,
 数列
数列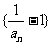 是以为
是以为 首项,
首项, 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)知 ,即
,即 ,
,
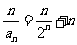 .
.
设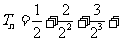 …
…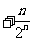 , ①
, ①
则 …
…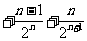 ,②
,②
由① ②得
②得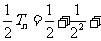 …
… ,
,

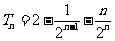 .又
.又 …
… .
.
 数列
数列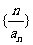 的前
的前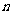 项和
项和

评注:解决数列问题就要判断是否为等差、等比数列,如果不是,那么能否构造新数列为特殊数列,注意转换角色,把数列问题转化为我们熟悉的特殊数列问题和研究方法解答。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com