
(1)理解不等式的性质及其证明.
(2)掌握两个正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
(3)掌握分析法、综合法、比较法证明简单的不等式.
(4)掌握简单不等式的解法.
(5)理解不等式│a│-│b│≤│a+b│≤│a│+│b│.
5、含绝对值的不等式.
4、不等式的证明
3、不等式的解法(特别一元二次不等式(特别是含参数)的解法).
2、不等式的基本性质
1、不等式.
6、作业:
(1)必做题:课本P82 A组第10题
(2)课外探究:利用计算机探索一般幂函数 的图象随
的图象随 的变化规律.
的变化规律.
[板书设计]
|
投 影 区 |
幂函数 一、定义 二、幂函数的图象与性质 |
三、例题及练习 |
5、小结:
通过本节的学习,你对幂函数有什么认识?你能概括一下吗?
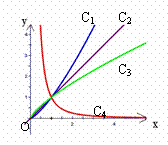
4、练习:如图所示,曲线C1、C2、C3、C4为幂函数 在第一象限内的图象,已知
在第一象限内的图象,已知 取
取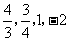 四个值,则相应于曲线C1、C2、C3、C4的解析式中的指数
四个值,则相应于曲线C1、C2、C3、C4的解析式中的指数 依次可取( )
依次可取( )
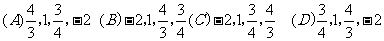
3、例题讲解:
 例:比较大小:
例:比较大小: 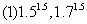 (2)
(2)
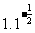 与
与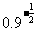
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com