
8.若集合A={1,m2},集合B={2,4},则“m=2”是“A∩B={4}”的 条件.
答案 充分不必要
7.(2008·天津理,6)设集合S={x||x-2|>3},T={x|a<x<a+8},S∪T=R,则a的取值范围是 .
答案 -3<a<-1
6.已知命题p: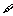 x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2},下列结论:
x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2},下列结论:
①命题“p∧q”是真命题;
②命题“p∧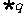 ”是假命题;
”是假命题;
③命题“ ”是真命题;
”是真命题;
④命题“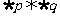 ”是假命题.
”是假命题.
其中正确的是 (填序号).
答案 ①②③④
5.设集合M={x|x>2},P={x|x<3},那么“x∈M或x∈P”是“x∈M∩P”的 条件.
答案 必要不充分
4.“a=2”是“直线ax+2y=0平行于直线x+y=1”的 条件.
答案 充要
3.(2009·江安中学第三次月考)已知集合N=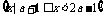 是集合M=
是集合M= 的子集,则a的取值范围为
.
的子集,则a的取值范围为
.
答案 2<a≤3
2.已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的 条件.
?答案 充分不必要
1.(2008·北京理,1) 已知全集U=R,集合A={x|-2≤x≤3},B={x|x<-1或x>4},那么集合A∩( uB)=
.
uB)=
.
答案 
(17)(本小题满分12分)
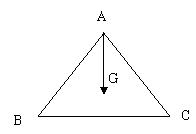
设G是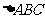 的重心(即三条中线的交点),
的重心(即三条中线的交点),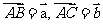 ,
,
(Ⅰ)试用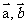 表示
表示 ;(Ⅱ)试用
;(Ⅱ)试用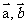 表示
表示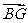
解:(Ⅰ)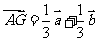 ----------------------------------(6分);
----------------------------------(6分);
(Ⅱ)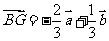 -----------------------------------(12分)
-----------------------------------(12分)
(18) (本小题满分12分)
已知函数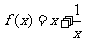
(Ⅰ)求证: 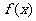 在区间
在区间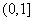 内单调递减,在
内单调递减,在 内单调递增;
内单调递增;
(Ⅱ)求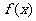 在区间
在区间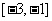 上的最小值.
上的最小值.
(Ⅰ)证明:设 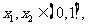 且
且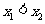 ,则
,则
又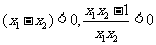
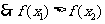
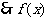 区间
区间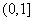 内单调递减,同理可证在
内单调递减,同理可证在 内单调递增;----------------------- (7分);
内单调递增;----------------------- (7分);
(Ⅱ)利用单调性的定义或奇函数的性质可知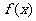 在区间
在区间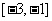 上单增,
上单增,
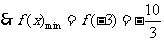 -----------------------------------------------------------------------------(12分)
-----------------------------------------------------------------------------(12分)
(19).(本小题满分12分)
已知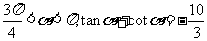
(Ⅰ)求 的值;
的值;
(Ⅱ)求的值.

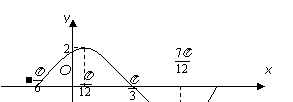 (20).(本小题满分12分)
(20).(本小题满分12分)
已知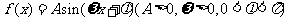
图象的一部分如图所示:
(1)求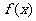 的解析式;(2)写出
的解析式;(2)写出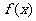 的单调区间.
的单调区间.
 (21).(本小题满分12分)
(21).(本小题满分12分)
舒城县某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:(1)当每辆车的月租金定为3600时,未租出的车辆数为: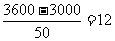 ,所以这时租出了88辆车。--------------------------------------------------------------------------------------------------------------- (4分);
,所以这时租出了88辆车。--------------------------------------------------------------------------------------------------------------- (4分);
(2)设每辆本的月租金定为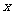 元,则租赁公司的月收益为:
元,则租赁公司的月收益为: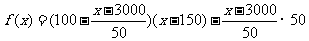 ,
,
整理得: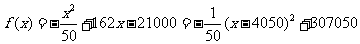 。所以,当
。所以,当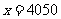 时,
时,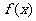 最大,其最大值为
最大,其最大值为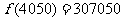 。即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元。--------------------------------------------------------------------------------------------------- (12分);
。即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元。--------------------------------------------------------------------------------------------------- (12分);
(22).(本小题满分14分)
已知: 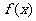 是定义在
是定义在 上的函数,且①
上的函数,且①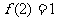 ,②对
,②对 ,恒有
,恒有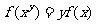 ③
③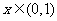 时,有
时,有
(Ⅰ)求证: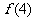 =2;
=2;
(Ⅱ)求证: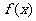 在
在 上单调递增。
上单调递增。
(Ⅲ)若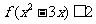 ,求
,求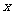 的取值范围。(提示:注意利用已证结论)
的取值范围。(提示:注意利用已证结论)
(13) 函数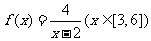 的值域为
。
的值域为
。
答案: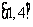

(14) 函数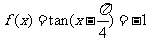 ,则
,则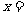 。
。
答案: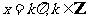
(15) 已知
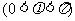 的图像关于直线
的图像关于直线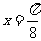 对称,则
对称,则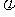 =
。
=
。
答案: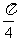
 (16) 设
(16) 设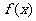 是R上的奇函数,且在
是R上的奇函数,且在 内是增函数,又
内是增函数,又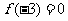 ,则
,则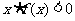 的解集是
。
的解集是
。
答案: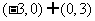
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com