
1.将植物栽培在适宜的光照、温度和充足的CO2条件下。如果将环境中CO2含量突然降至极低水平.此时叶肉细胞内的C3化合物、C5化合物和ATP含量的变化情况依次是( )
A.上升;下降;上升 B.下降;上升;下降
C.下降;上升;上升 D.上升;下降:下降
22.(本题满分14分)
设函数 ,其中
,其中
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)是否存在负数 ,使
,使 对一切正数
对一切正数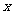 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
21.(本小题满分14分)
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
(1)求证:B1D⊥平面ABD;
(2)求异面直线BD与EF所成的角;
(3)求点F到平面ABD的距离。

20.(本题满分12分)
已知数列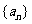 的前
的前 项和为
项和为 ,且
,且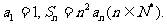
(1)求 的值;
的值;
(2)猜想 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
19.(本小题满分12分)
某公司在“2010年上海世博会知识宣传”活动中进行抽奖活动,抽奖规则是:在一个盒子中装有8张大小相同的精美卡片,其中2张印有“世博会欢迎您”字样,2张印有“世博会会徽”图案,4张印有“海宝”(世博会吉祥物)图案,现从盒子里无放回的摸取卡片,找出印有“海宝”图案的卡片表示中奖且停止摸卡。
(Ⅰ)求最多摸两次中奖的概率;
(Ⅱ)用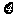 表示摸卡的次数,求
表示摸卡的次数,求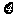 的分布列和数学期望。
的分布列和数学期望。
18.(本小题满分12分)
已知 是奇函数,且在定义域(-1,1)内可导并满足
是奇函数,且在定义域(-1,1)内可导并满足 解关于m的不等式
解关于m的不等式
17.(本小题满分12分)
已知合集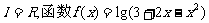 的定义域为M,
的定义域为M, ,若
,若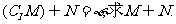
16.以下四个命题:
①如果两个平面垂直,则其中一个平面内的任意一条直线
都垂直于另一个平面内无数条直线;②设m、n为两条不
同的直线, 、
、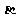 是两个不同的平面,若
是两个不同的平面,若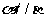 ,
, ,③“直线
,③“直线 ”的充分而不必要条件是“
”的充分而不必要条件是“ 垂直于
垂直于 在平面
在平面 内的射影”;④若点P到一个三角形三条边的距离相等,则点P在该三角形所在平面上的射影是该三角形的内心。其中正确的命题序号为 。
内的射影”;④若点P到一个三角形三条边的距离相等,则点P在该三角形所在平面上的射影是该三角形的内心。其中正确的命题序号为 。
15. 为了了解高三学生的身体状况,抽取了部分男生的体重,
为了了解高三学生的身体状况,抽取了部分男生的体重,
将所得的数据整理后,画出了频率分布直方图(如下左
图),已知图中从左到右的前3个小组的频率比为1:2:
3,第2小组的频数为12,则抽取的男生人数是 。
14.标准正态总体的函数表达式是 ,则
,则 的单调减区间是
。
的单调减区间是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com