
4.了解复合函数的概念。会将一个函数的复合过程进行分解或将几个函数进行复合。掌握复合函数的求导法则,并会用法则解决一些简单问题。
3.了解函数的和、差、积的求导法则的推导,掌握两个函数的商的求导法则。能正确运用函数的和、差、积的求导法则及已有的导数公式求某些简单函数的导数。
1.了解导数的概念,能利用导数定义求导数.掌握函数在一点处的导数的定义和导数的几何意义,理解导函数的概念.了解曲线的切线的概念.在了解瞬时速度的基础上抽象出变化率的概念.
2 熟记基本导数公式(c,x
熟记基本导数公式(c,x (m为有理数),sin x, cos x, e
(m为有理数),sin x, cos x, e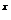 , a
, a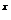 , lnx, log
, lnx, log x的导数)。掌握两个函数四则运算的求导法则和复合函数的求导法则,会求某些简单函数的导数,利能够用导数求单调区间,求一个函数的最大(小)值的问题,掌握导数的基本应用.
x的导数)。掌握两个函数四则运算的求导法则和复合函数的求导法则,会求某些简单函数的导数,利能够用导数求单调区间,求一个函数的最大(小)值的问题,掌握导数的基本应用.
⑴了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等),掌握函数在一点处的导数的定义和导数的几何意义,理解导函数的概念。
⑵熟记基本导数公式(c,x (m为有理数),sin x, cos x, e
(m为有理数),sin x, cos x, e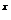 , a
, a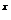 ,lnx, log
,lnx, log x的导数)。掌握两个函数四则运算的求导法则和复合函数的求导法则,会求某些简单函数的导数。
⑶了解可导函数的单调性与其导数的关系,了解可导函数在某点取得极值的必要条件和充分条件(导数要极值点两侧异号),会求一些实际问题(一般指单峰函数)的最大值和最小值。
x的导数)。掌握两个函数四则运算的求导法则和复合函数的求导法则,会求某些简单函数的导数。
⑶了解可导函数的单调性与其导数的关系,了解可导函数在某点取得极值的必要条件和充分条件(导数要极值点两侧异号),会求一些实际问题(一般指单峰函数)的最大值和最小值。
19.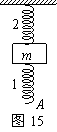 (16分)如图15所示,质量为m的物体被劲度系数为k2的弹簧2悬挂在天花板上,下面还拴着劲度系数为k1的轻弹簧1,托住下弹簧的端点A用力向上压,当弹簧2的弹力大小为
(16分)如图15所示,质量为m的物体被劲度系数为k2的弹簧2悬挂在天花板上,下面还拴着劲度系数为k1的轻弹簧1,托住下弹簧的端点A用力向上压,当弹簧2的弹力大小为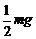 时,弹簧1的下端点A上移的高度是多少?
时,弹簧1的下端点A上移的高度是多少?
18. (10分)如图14所示,小球的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于小球上,AC绳水平。在小球上另施加一个方向与水平线成θ=60º角的拉力F,若要使绳子都能伸直,求拉力F的大小范围。
(10分)如图14所示,小球的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于小球上,AC绳水平。在小球上另施加一个方向与水平线成θ=60º角的拉力F,若要使绳子都能伸直,求拉力F的大小范围。
17.(10分)重力G=40N的物体,与竖直墙壁间的动摩擦因数μ=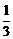 ,若用斜向上的F=50N的推力托住物体,使物体处于静止,如图13所示,求这时物体受到的摩擦力是多大?要使物体能匀速下滑,推力F的大小应变为多大?(sin53º=0.8,cos53º=0.6)
,若用斜向上的F=50N的推力托住物体,使物体处于静止,如图13所示,求这时物体受到的摩擦力是多大?要使物体能匀速下滑,推力F的大小应变为多大?(sin53º=0.8,cos53º=0.6)
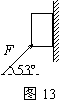
16. 有两个光滑球,半径均为r=3cm,重均为8N,静止在半径为R=8cm的光滑半球形碗底,如图12所示。两球间的相互作用力的大小为_______N。当碗的半径增大时,两球间的相互作用力变___________,球对碗的压力变___________(填“大”或“小”)。
有两个光滑球,半径均为r=3cm,重均为8N,静止在半径为R=8cm的光滑半球形碗底,如图12所示。两球间的相互作用力的大小为_______N。当碗的半径增大时,两球间的相互作用力变___________,球对碗的压力变___________(填“大”或“小”)。
15.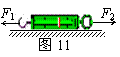 如图11所示,一个准确的弹簧秤,置于粗糙的水平地面上,用F1=5N的水平力拉秤钩,用F2=6N的水平力拉另一端的圆环,弹簧秤处于静止状态。这时弹簧秤受到的静摩擦力大小是_______N,方向___________。弹簧秤的示数为_______N。
如图11所示,一个准确的弹簧秤,置于粗糙的水平地面上,用F1=5N的水平力拉秤钩,用F2=6N的水平力拉另一端的圆环,弹簧秤处于静止状态。这时弹簧秤受到的静摩擦力大小是_______N,方向___________。弹簧秤的示数为_______N。
14. 如图10所示,完全相同的A、B两物体放在水平面上,物体与水平面间的动摩擦因数均为0.2,每个物体重G=10N,设两物体与水平面间的最大静摩擦力均为2.5N。若对A施加一个由零均匀增大到6N的水平推力F,则A所受的摩擦力F1随推力F变化的情况请在图中作出。
如图10所示,完全相同的A、B两物体放在水平面上,物体与水平面间的动摩擦因数均为0.2,每个物体重G=10N,设两物体与水平面间的最大静摩擦力均为2.5N。若对A施加一个由零均匀增大到6N的水平推力F,则A所受的摩擦力F1随推力F变化的情况请在图中作出。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com