
1.匀减速运动物体追匀速直线运动物体。
①两者v相等时,S追<S被追 永远追不上,但此时两者的距离有最小值
②若S追<S被追、V追=V被追 恰好追上,也是恰好避免碰撞的临界条件。追 被追
③若位移相等时,V追>V被追则还有一次被追上的机会,其间速度相等时,两者距离有一个极大值
4、匀变速直线运动
(1)深刻理解:

(2)公式 (会“串”起来)

①根据平均速度定义 =
= =
=
∴Vt/ 2 = =
=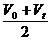 =
=
②根据基本公式得Ds = aT2  一
一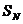 =3 aT2 Sm一Sn=(
m-n) aT2
=3 aT2 Sm一Sn=(
m-n) aT2
推导:
第一个T内
 第二个T内
第二个T内
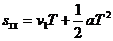 又
又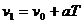
∴Ds =SⅡ-SⅠ=aT2
以上公式或推论,适用于一切匀变速直线运动,记住一定要规定正方向!选定参照物!同学要求必须会推导,只有亲自推导过,印象才会深刻!
(3) 初速为零的匀加速直线运动规律
①在1T末 、2T末、3T末……ns末的速度比为1:2:3……n;
②在1T 、2T、3T……nT内的位移之比为12:22:32……n2;
③在第1T 内、第 2T内、第3T内……第nT内的位移之比为1:3:5……(2n-1); (各个相同时间间隔均为T)
④从静止开始通过连续相等位移所用时间之比为1: :
: ……(
……(
⑤通过连续相等位移末速度比为1: :
: ……
……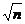
(4) 匀减速直线运动至停可等效认为反方向初速为零的匀加速直线运动.(由竖直上抛运动的对称性得到的启发)。(先考虑减速至停的时间).
(5)竖直上抛运动:(速度和时间的对称)
分过程:上升过程匀减速直线运动,下落过程初速为0的匀加速直线运动.
全过程:是初速度为V0加速度为-g的匀减速直线运动。适用全过程S = Vo t - g t2 ;
Vt = Vo-g t ; Vt2-Vo2 = -2gS (S、Vt的正、负号的理解)
g t2 ;
Vt = Vo-g t ; Vt2-Vo2 = -2gS (S、Vt的正、负号的理解)
上升最大高度:H =  上升的时间:t=
上升的时间:t= 
对称性:
①上升、下落经过同一位置时的加速度相同,而速度等值反向
②上升、下落经过同一段位移的时间相等  。从抛出到落回原位置的时间:t =2
。从抛出到落回原位置的时间:t =2
(6)图像问题
识图方法:一轴物理量、二单位、三物理意义(斜率、面积、截距、交点等)
图像法是物理学研究常用的数学方法。用它可直观表达物理规律,可帮助人们发现物理规律。借用此法还能帮助人们解决许许多多物理问题。对于诸多运动学、动力学问题特别是用物理分析法(公式法)难以解决的问题,若能恰当地运用运动图像处理,则常常可使运动过程、状态更加清晰、求解过程大为简化。请叙述下列图象的意义.
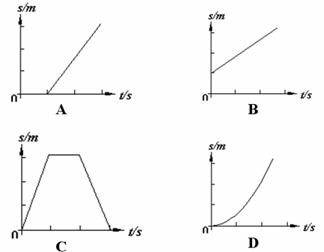
①、位移-时间图象(s-t图像):
横轴表示时间,纵轴表示位移;
静止的s-t图像在一条与横轴平行或重合的直线上;
匀速直线运动的s-t图像在一条倾斜直线上,所在直线的斜率表示运动速度的大小及符号;
②、速度-时间图像(v-t图像):
横轴表示时,纵轴表示速度;请叙述下列图象的意义.
静止的v-t图像在一条与横轴重合的直线上;
匀速直线运动的v-t图像在一条与横轴平行的直线上;
匀变速直线运的v-t图像在一条倾斜直线上,所在直线的斜率表示加速度大小及符号;
 当直线斜率(加速度)与运动速度同号时,物体做匀加速直线运动;
当直线斜率(加速度)与运动速度同号时,物体做匀加速直线运动;
当直线余率(加速度)与运动速度异号时,物体做匀减速直线运动。
匀变速直线运的v-t图像在一条倾斜直线上,面积表示位移
(7)追及和相遇或避免碰撞的问题的求解方法:
关键:在于掌握两个物体的位置坐标及相对速度的特殊关系。
基本思路:分别对两个物体研究,画出运动过程示意图,列出方程,找出时间、速度、位移的关系。解出结果,必要时进行讨论。
追及条件:追者和被追者v相等是能否追上、两者间的距离有极值、能否避免碰撞的临界条件。
讨论:
3、分类

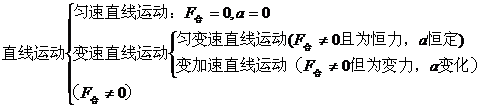
2、基本概念
(1) (2)
(2) (3)
(3)
(4)
1、直线运动的条件:①F合=0或②F合≠0且F合与v共线,a与v共线。(回忆曲线运动的条件)
13、
解析:设卡车的质量为M,车所受阻力与车重之比为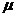 ;刹车前卡车牵引力的大小为
;刹车前卡车牵引力的大小为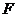 ,
,
卡车刹车前后加速度的大小分别为 和
和 。重力加速度大小为g。由牛顿第二定律有
。重力加速度大小为g。由牛顿第二定律有
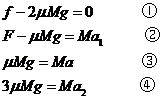
设车厢脱落后,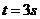 内卡车行驶的路程为
内卡车行驶的路程为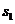 ,末速度为
,末速度为 ,根据运动学公式有
,根据运动学公式有
 ⑤
⑤
 ⑥
⑥
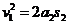 ⑦
⑦
式中,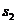 是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为
是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为 ,有
,有
 ⑧
⑧
卡车和车厢都停下来后相距 ⑨
⑨
由①至⑨式得 10
10
带入题给数据得 11
11
评分参考:本题9分。①至⑧式各1分,11式1分
12、
解析:
 (1)第一次飞行中,设加速度为
(1)第一次飞行中,设加速度为
匀加速运动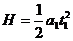
由牛顿第二定律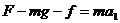
解得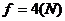
(2)第二次飞行中,设失去升力时的速度为 ,上升的高度为
,上升的高度为
匀加速运动
设失去升力后的速度为 ,上升的高度为
,上升的高度为
由牛顿第二定律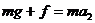
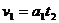

解得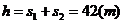
(3)设失去升力下降阶段加速度为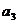 ;恢复升力后加速度为
;恢复升力后加速度为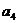 ,恢复升力时速度为
,恢复升力时速度为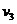
由牛顿第二定律

F+f-mg=ma4
且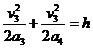
V3=a3t3
解得t3=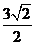 (s)(或2.1s)
(s)(或2.1s)
11、答案:440N,275N
解析:解法一:(1)设运动员受到绳向上的拉力为F,由于跨过定滑轮的两段绳子拉力相等,吊椅受到绳的拉力也是F。对运动员和吊椅整体进行受力分析如图所示,则有:
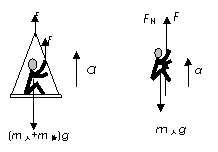
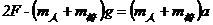

由牛顿第三定律,运动员竖直向下拉绳的力
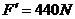
(2)设吊椅对运动员的支持力为FN,对运动员进行受力分析如图所示,则有:
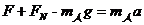
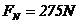
由牛顿第三定律,运动员对吊椅的压力也为275N
解法二:设运动员和吊椅的质量分别为M和m;运动员竖直向下的拉力为F,对吊椅的压力大小为FN。
根据牛顿第三定律,绳对运动员的拉力大小为F,吊椅对运动员的支持力为FN。分别以运动员和吊椅为研究对象,根据牛顿第二定律
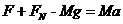 ①
①
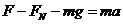 ②
②
由①②得 

10、解析:(1)设货物滑到圆轨道末端是的速度为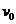 ,对货物的下滑过程中根据机械能守恒定律得,
,对货物的下滑过程中根据机械能守恒定律得, ①
①
设货物在轨道末端所受支持力的大小为 ,根据牛顿第二定律得,
,根据牛顿第二定律得, ②
②
联立以上两式代入数据得 ③
③
根据牛顿第三定律,货物到达圆轨道末端时对轨道的压力大小为3000N,方向竖直向下。
(2)若滑上木板A时,木板不动,由受力分析得 ④
④
若滑上木板B时,木板B开始滑动,由受力分析得 ⑤
⑤
联立④⑤式代入数据得 ⑥。
⑥。
(3)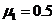 ,由⑥式可知,货物在木板A上滑动时,木板不动。设货物在木板A上做减速运动时的加速度大小为
,由⑥式可知,货物在木板A上滑动时,木板不动。设货物在木板A上做减速运动时的加速度大小为 ,由牛顿第二定律得
,由牛顿第二定律得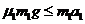 ⑦
⑦
设货物滑到木板A末端是的速度为 ,由运动学公式得
,由运动学公式得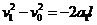 ⑧
⑧
联立①⑦⑧式代入数据得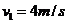 ⑨
⑨
设在木板A上运动的时间为t,由运动学公式得 ⑩
⑩
联立①⑦⑨⑩式代入数据得 。
。
考点:机械能守恒定律、牛顿第二定律、运动学方程、受力分析
9、
答案:BC
解析:受力分析可知,下滑时加速度为 ,上滑时加速度为
,上滑时加速度为 ,所以C正确。设下滑的距离为l,根据能量守恒有
,所以C正确。设下滑的距离为l,根据能量守恒有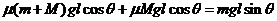 ,得m=2M。也可以根据除了重力、弹性力做功以外,还有其他力(非重力、弹性力)做的功之和等于系统机械能的变化量,B正确。在木箱与货物从顶端滑到最低点的过程中,减少的重力势能转化为弹簧的弹性势能和内能,所以D不正确。
,得m=2M。也可以根据除了重力、弹性力做功以外,还有其他力(非重力、弹性力)做的功之和等于系统机械能的变化量,B正确。在木箱与货物从顶端滑到最低点的过程中,减少的重力势能转化为弹簧的弹性势能和内能,所以D不正确。
考点:能量守恒定律,机械能守恒定律,牛顿第二定律,受力分析
提示:能量守恒定律的理解及应用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com