
2.光速  21世纪教育网
21世纪教育网
光在真空中的转播速度为c=3.00×108m/s。 21世纪教育网
21世纪教育网
⑴光在不同介质中的传播速度是不同的。根据爱因斯坦的相对论光速不可能超过c。 21世纪教育网
21世纪教育网
⑵近年来(1999-2001年)科学家们在极低的压强(10-9Pa)和极低的温度(10-9K)下,得到一种物质的凝聚态,光在其中的速度降低到17m/s,甚至停止运动。 21世纪教育网
21世纪教育网
⑶也有报道称在实验中测得的光速达到1011m/s,引起物理学界的争论。 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 例题分析
例题分析 21世纪教育网
21世纪教育网
例:如图所示,在A点有一个小球,紧靠小球的左方有一个点光源S。现将小球从A点正对着竖直墙平抛出去,打到竖直墙之前,小球在点光源照射下的影子在墙上的运动是  21世纪教育网
21世纪教育网
A.匀速直线运动 B.自由落体运动 21世纪教育网
21世纪教育网
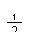 C.变加速直线运动 D.匀减速直线运动
C.变加速直线运动 D.匀减速直线运动 21世纪教育网
21世纪教育网
解:小球抛出后做平抛运动,时间t后水平位移是vt,竖直位移是h= gt2,根据相似形知识可以由比例求得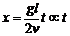 ,因此影子在墙上的运动是匀速运动。
,因此影子在墙上的运动是匀速运动。 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
目的要求 21世纪教育网
21世纪教育网
复习光在媒质中的传播和光速。 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
知识要点 21世纪教育网
21世纪教育网
1.光在同一种均匀介质中是沿直线传播的。 21世纪教育网
21世纪教育网
前提条件是在同一种介质,而且是均匀介质。否则,可能发生偏折。如光从空气斜射入水中(不是同一种介质);“海市蜃楼”现象(介质不均匀)。 21世纪教育网
21世纪教育网
当障碍物或孔的尺寸和波长可以相比或者比波长小时,将发生明显的衍射现象,光线将可能偏离原来的传播方向。 21世纪教育网
21世纪教育网
解光的直线传播方面的计算题(包括日食、月食、本影、半影问题)关键是画好示意图,利用数学中的相似形等几何知识计算。 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
 21世纪教育网
21世纪教育网
§1.几何光学 21世纪教育网
21世纪教育网
24.解:(1)解法1:根据题意可得:A(-1,0),B(3,0);
则设抛物线的解析式为 (a≠0)
(a≠0)
又点D(0,-3)在抛物线上,∴a(0+1)(0-3)=-3,解之得:a=1
∴y=x2-2x-3····································································································· 3分
自变量范围:-1≤x≤3···················································································· 4分
解法2:设抛物线的解析式为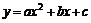 (a≠0)
(a≠0)
根据题意可知,A(-1,0),B(3,0),D(0,-3)三点都在抛物线上
∴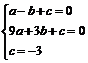 ,解之得:
,解之得: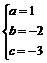
∴y=x2-2x-3····································································································· 3分
自变量范围:-1≤x≤3······························································ 4分
(2)设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,
在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=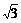
在Rt△MCE中,∵OC=2,∠CMO=60°,∴ME=4
∴点C、E的坐标分别为(0,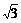 ),(-3,0) ·················································· 6分
),(-3,0) ·················································· 6分
∴切线CE的解析式为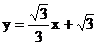 ··························································· 8分
··························································· 8分
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ·························· 9分
由题意可知方程组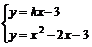 只有一组解
只有一组解
即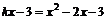 有两个相等实根,∴k=-2·············································· 11分
有两个相等实根,∴k=-2·············································· 11分
∴过点D“蛋圆”切线的解析式y=-2x-3····················································· 12分
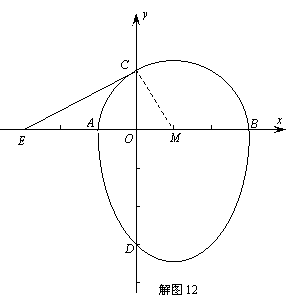
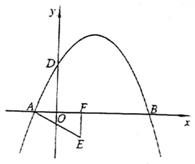
24.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
如图12,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;
(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.
(08湖南益阳24题解析)七、(本题12分)
12.(08湖南长沙)26.如图,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.
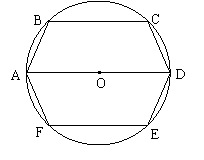 (1)当∠BAD=75°时,求的长;
(1)当∠BAD=75°时,求的长;
(2)求证:BC∥AD∥FE;
(3)设AB=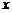 ,求六边形ABCDEF的周长L关于
,求六边形ABCDEF的周长L关于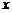 的函数关系式,并指出
的函数关系式,并指出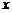 为何值时,L取得最大值.
为何值时,L取得最大值.
(08湖南长沙26题解析)26.(1)连结OB、OC,由∠BAD=75°,OA=OB知∠AOB=30°, (1分)
∵AB=CD,∴∠COD=∠AOB=30°,∴∠BOC=120°,······································ (2分)
故的长为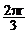 .··························································································· (3分)
.··························································································· (3分)
(2)连结BD,∵AB=CD,∴∠ADB=∠CBD,∴BC∥AD,······························· (5分)
同理EF∥AD,从而BC∥AD∥FE.································································ (6分)
(3)过点B作BM⊥AD于M,由(2)知四边形ABCD为等腰梯形,
从而BC=AD-2AM=2r-2AM.··········································································· (7分)
∵AD为直径,∴∠ABD=90°,易得△BAM∽△DAB
∴AM=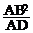 =
=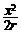 ,∴BC=2r-
,∴BC=2r- ,同理EF=2r-
,同理EF=2r- ············································ (8分)
············································ (8分)
∴L=4x+2(2r- )=
)=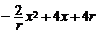 =
=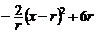 ,其中0<x<
,其中0<x<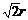 ·········· (9分)
·········· (9分)
∴当x=r时,L取得最大值6r.······································································ (10分)
13(08湖南益阳)七、(本题12分)
11.(08湖北咸宁)24.(本题(1)-(3)小题满分12分,(4)小题为附加题另外附加2分)
如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
(1) 当P点在边AB上运动时,点Q的横坐标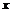 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2) 求正方形边长及顶点C的坐标;
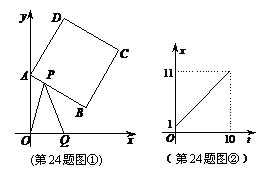 (3) 在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(3) 在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(1) 附加题:(如果有时间,还可以继续
解答下面问题,祝你成功!)
如果点P、Q保持原速度速度不
变,当点P沿A→B→C→D匀
速运动时,OP与PQ能否相等,
若能,写出所有符合条件的t的
值;若不能,请说明理由.
(08湖北咸宁24题解析)24.解:(1)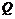 (1,0)
-----------------------------1分
(1,0)
-----------------------------1分
点P运动速度每秒钟1个单位长度.-------------------------------3分
(2) 过点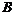 作BF⊥y轴于点
作BF⊥y轴于点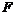 ,
,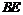 ⊥
⊥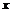 轴于点
轴于点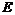 ,则
,则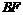 =8,
=8,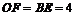 .
.
∴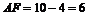 .
.
在Rt△AFB中,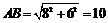 .----------------------------5分
.----------------------------5分
过点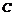 作
作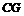 ⊥
⊥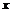 轴于点
轴于点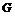 ,与
,与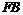 的延长线交于点
的延长线交于点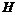 .
.
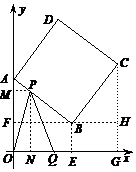 ∵
∵ ∴△ABF≌△BCH.
∴△ABF≌△BCH.
∴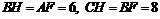 .
.
∴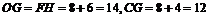 .
.
∴所求C点的坐标为(14,12).------------7分
(3) 过点P作PM⊥y轴于点M,PN⊥ 轴于点N,
轴于点N,
则△APM∽△ABF.
∴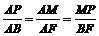 .
. 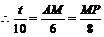 .
.
∴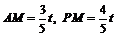 . ∴
. ∴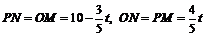 .
.
设△OPQ的面积为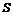 (平方单位)
(平方单位)
∴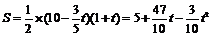 (0≤
(0≤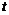 ≤10)
------------------10分
≤10)
------------------10分
说明:未注明自变量的取值范围不扣分.
∵ <0 ∴当
<0 ∴当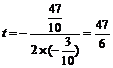 时, △OPQ的面积最大.------------11分
时, △OPQ的面积最大.------------11分
此时P的坐标为(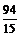 ,
, ) .
---------------------------------12分
) .
---------------------------------12分
(4)
当 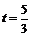 或
或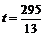 时, OP与PQ相等.---------------------------14分
时, OP与PQ相等.---------------------------14分
对一个加1分,不需写求解过程.
10.(08湖北武汉)(本题答案暂缺)25.(本题 12分)如图 1,抛物线y=ax2-3ax+b经过A(-1,0),C(3,2)两点,与y轴交于点D,与x轴交于另一点B.(1)求此抛物线的解析式;(2)若直线y=kx-1(k≠0)将 四 边 形ABCD面积二等分,求k的值;(3)如图2,过点 E(1,-1)作EF⊥x轴于点F,将△AEF绕平面内某点旋转 180°后得△MNQ(点M,N,Q分别与 点 A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.
(08湖北武汉25题解析)25.⑴ ;⑵
;⑵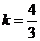 ;⑶M(3,2),N(1,3)
;⑶M(3,2),N(1,3)
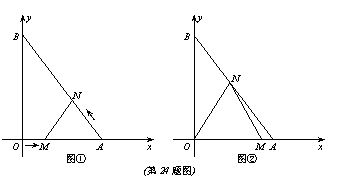
9.(08湖北天门)(本题答案暂缺)24.(本小题满分12分)如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒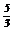 个单位长度的速度向终点B运动.设运动了x秒.
个单位长度的速度向终点B运动.设运动了x秒.
(1)点N的坐标为(________________,________________);(用含x的代数式表示)
(2)当x为何值时,△AMN为等腰三角形?
(3)如图②,连结ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度和此时x的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com