
4.若是第三象限角,则下列各式中不成立的是………………(B)
A:sina+cosa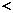 0
B:tana-sina
0
B:tana-sina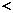 0
0
C:cosa-cota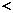 0
D:cotacsca
0
D:cotacsca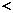 0
0
3.若三角形的两内角a,b满足sinacosb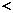 0,则此三角形必为……(B)
0,则此三角形必为……(B)
A锐角三角形 B钝角三角形 C直角三角形 D以上三种情况都可能
2. .x取什么值时,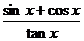 有意义?
有意义?
分析:因为正弦、余弦函数的定义域为R,故只要考虑正切函数的定义域和分式的分母不能为零.
解:由题意得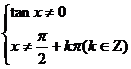 解得:
解得: 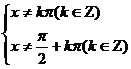
即: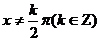
所以,当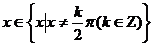 时,
时,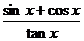 有意义.
有意义.
1.确定下列各式的符号
(1)sin100°·cos240° (2)sin5+tan5
分析:由角所在象限分别判断两个三角函数值的符号,再确定各式的符号.
解(1)∵100°是第二象限的角,240°是第三象限的角.
∴sin100°>0,cos240°<0,于是有sin100°·cos240°<0.
(2)∵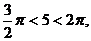 ∴5是第四象限的角
∴5是第四象限的角
∴sin5<0,tan5<0,于是有sin5+tan5<0.
例1 确定下列三角函数值的符号
(1)cos250° (2)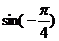 (3)tan(-672°) (4)
(3)tan(-672°) (4)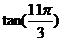
解:(1)∵250°是第三象限角 ∴cos250°<0
(2)∵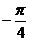 是第四象限角,∴
是第四象限角,∴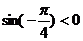
(3)tan(-672°)=tan(48°-2×360°)=tan48°
而48°是第一象限角,∴tan(-672°)>0
(4) 
而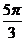 是第四象限角,∴
是第四象限角,∴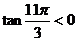 .
.
例2 求证角θ为第三象限角的充分必要条件是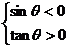
证明:必要性:∵θ是第三象限角,
∴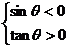
充分性:∵sinθ<0,
∴θ是第三或第四象限角或终边在y轴的非正半轴上
∵tanθ>0,∴θ是第一或第三象限角.
∵sinθ<0,tanθ>0都成立.
∴θ为第三象限角.
例3 求下列三角函数的值
(1)sin1480°10′ (2)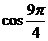 (3)
(3)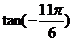 .
.
解:(1)sin1480°10′=sin(40°10′+4×360°)
=Sin40°10′=0.6451
(2) 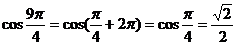
(3)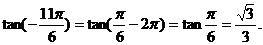
例4 求值:sin(-1320°)cos1110°+cos(-1020°)sin750°+tg4950°.
解:原式=sin(-4×360°+120°)·cos(3×360°+30°)
+cos(-3×360°+60°)sin(2×360°+30°)+tg(360°+135°).
=sin120°·cos30°+cos60°·sin30°+tg135°
= -1=0
-1=0
2. 终边相同的角的同一三角函数值相等
例如390°和-330°都与30°终边位置相同,由三角函数定义可知它们的三角函数值相同,即
sin390°=sin30° cos390°=cos30°
sin(-330°)=sin30° cos(-330°)=cos30°
诱导公式一(其中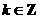 ): 用弧度制可写成
): 用弧度制可写成
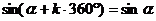
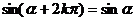
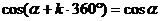
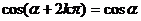
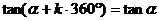
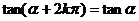
这组公式的作用是可把任意角的三角函数值问题转化为0-2π间角的三角函数值问题.
1. 三角函数在各象限内的符号规律:
第一象限: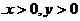
∴sina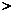 0,cosa
0,cosa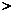 0,tana
0,tana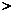 0,cota
0,cota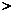 0,seca
0,seca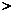 0,csca
0,csca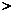 0
0
第二象限:
∴sina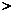 0,cosa
0,cosa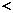 0,tana
0,tana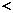 0,cota
0,cota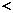 0,seca
0,seca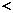 0,csca
0,csca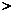 0
0
第三象限: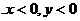
∴sina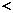 0,cosa
0,cosa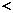 0,tana
0,tana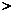 0,cota
0,cota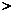 0,seca
0,seca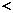 0,csca
0,csca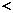 0
0
第四象限: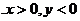
∴sina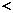 0,cosa
0,cosa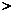 0,tana
0,tana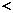 0,cota
0,cota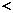 0,seca
0,seca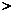 0,csca
0,csca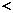 0
0
记忆法则:
第一象限全为正,二正三切四余弦.
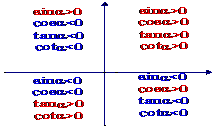
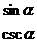 为正 全正
为正 全正
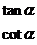 为正
为正  为正
为正
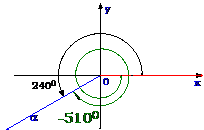
4.注意:
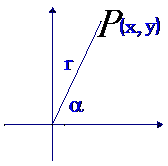
(1)以后我们在平面直角坐标系内研究角的问题,其顶点都在原点,始边都与x轴的非负半轴重合.
(2)OP是角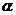 的终边,至于是转了几圈,按什么方向旋转的不清楚,也只有这样,才能说明角
的终边,至于是转了几圈,按什么方向旋转的不清楚,也只有这样,才能说明角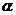 是任意的.
是任意的.
(3)sin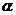 是个整体符号,不能认为是“sin”与“
是个整体符号,不能认为是“sin”与“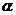 ”的积.其余五个符号也是这样.
”的积.其余五个符号也是这样.
(4)定义中只说怎样的比值叫做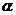 的什么函数,并没有说
的什么函数,并没有说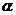 的终边在什么位置(终边在坐标轴上的除外),即函数的定义与
的终边在什么位置(终边在坐标轴上的除外),即函数的定义与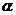 的终边位置无关.
的终边位置无关.
(5)比值只与角的大小有关.
3.突出探究的几个问题:
①角是“任意角”,当b=2kp+a(kÎZ)时,b与a的同名三角函数值应该是相等的,即凡是终边相同的角的三角函数值相等
②实际上,如果终边在坐标轴上,上述定义同样适用
③三角函数是以“比值”为函数值的函数
④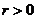 而x,y的正负是随象限的变化而不同,故三角函数的符号应由象限确定.
而x,y的正负是随象限的变化而不同,故三角函数的符号应由象限确定.
⑤定义域:
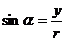 R
R
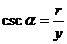
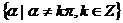
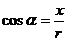 R
R
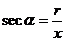
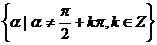
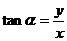
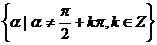
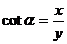
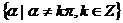
2. 比值
比值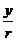 叫做
叫做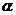 的正弦 记作:
的正弦 记作: 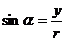
比值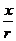 叫做
叫做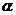 的余弦 记作:
的余弦 记作: 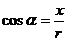
比值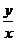 叫做
叫做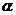 的正切 记作:
的正切 记作: 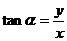
比值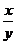 叫做
叫做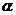 的余切 记作:
的余切 记作: 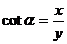
比值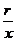 叫做
叫做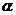 的正割 记作:
的正割 记作: 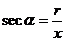
比值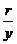 叫做
叫做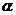 的余割 记作:
的余割 记作: 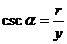
以上六种函数,统称为三角函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com