
13.已知椭圆C: (
( ),其离心率为
),其离心率为 ,两准线之间的距离为
,两准线之间的距离为 。(1)求
。(1)求 之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
解:(1)设c为椭圆的焦半径,则 . ……………………(5分)
. ……………………(5分)
于是有a=5,b=3.
(2) 解法一:设B点坐标为 ,P点坐标为
,P点坐标为 .于是有
.于是有
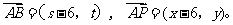
因为 ,所以有
,所以有 .
(A1 )
.
(A1 )
又因为ABP为等腰直角三角形,所以有 AB=AP,即
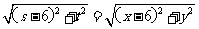 .
(A2 ) …………(10分)
.
(A2 ) …………(10分)
由(A1)推出 ,代入(A2),得
,代入(A2),得 ……(15分)
……(15分)
从而有  ,即
,即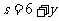 (不合题意,舍去)或
(不合题意,舍去)或 .
.
代入椭圆方程,即得动点P的轨迹方程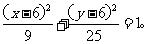 …………(20分)
…………(20分)
解法二: 设 ,
, ,则以A为圆心,r为半径的圆的参数方程为
,则以A为圆心,r为半径的圆的参数方程为
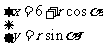 .
.
设AB与x轴正方向夹角为 ,B点的参数表示为
,B点的参数表示为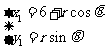 , …………(10分)
, …………(10分)
P点的参数表示为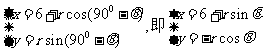 .
.
从上面两式,得到 . ……………………(15分)
. ……………………(15分)
又由于B点在椭圆上,可得 . ……………………(20分)
. ……………………(20分)
此即为P点的轨迹方程.
12.在边长为1的正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上.AD的长度的最小值为 .
解:设 ,作△ADE关于DE的对称图形,A的对称点G落在BC上.在△DGB中,
,作△ADE关于DE的对称图形,A的对称点G落在BC上.在△DGB中,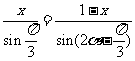

当 时,即
时,即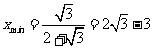 .
.
11.已知 ,直线
,直线 与
与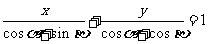
的交点在直线 上,则
上,则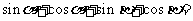 .
.
解:由已知可知,可设两直线的交点为 ,且
,且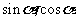 为方程
为方程
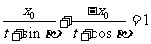 ,
,
的两个根,即为方程
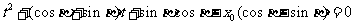
的两个根.因此
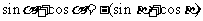 ,
,
即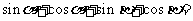 0.
0.
10. 设实系数一元二次方程 有两个相异实根,其中一根在区间
有两个相异实根,其中一根在区间 内,另一根在区间
内,另一根在区间 内,则
内,则 的取值范围是
.
的取值范围是
.
解: 根据题意,设两个相异的实根为 ,且
,且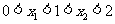 ,则
,则
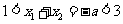 ,
, .
.
于是有 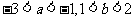 ,也即有
,也即有
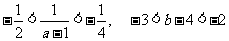 .
.
故有 ,即取值范围为
,即取值范围为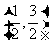 .
.
9.设 ,则
,则 .
.
解: 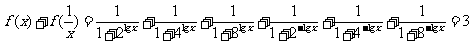 .
.
8.设 为非负实数,满足
为非负实数,满足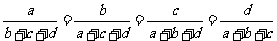 ,则
,则
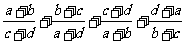 =
.
=
.
解:显然 ,由于
,由于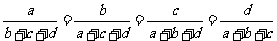 ,有
,有
 .于是有
.于是有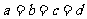 ,故
,故
 .
.
7. = .
= .
解:根据题意要求, ,
, .于是有
.于是有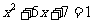 .因此
.因此
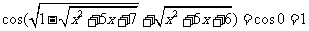 .因此答案为 1.
.因此答案为 1.
6.圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为SO的中点,动点P在圆锥底面内(包括圆周).若AM⊥MP,则P点形成的轨迹的长度为( )
A.  B.
B.  C. 3
D.
C. 3
D.
解:建立空间直角坐标系.设A(0,-1,0), B(0,1,0), ,
,  ,P(x,y,0).于是有
,P(x,y,0).于是有 由于AM⊥MP,所以
由于AM⊥MP,所以
 ,即
,即 ,此为P点形成的轨迹方程,其在底面圆盘内的长度为
,此为P点形成的轨迹方程,其在底面圆盘内的长度为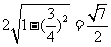 . 因此 选 B.
. 因此 选 B.
5.已知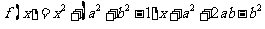 是偶函数,则函数图象与
是偶函数,则函数图象与 轴交点的纵坐标的最大值是( )
轴交点的纵坐标的最大值是( )
A.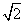 B. 2 C.
B. 2 C.  D. 4
D. 4
解:由已知条件可知,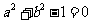 ,函数图象与
,函数图象与 轴交点的纵坐标为
轴交点的纵坐标为 .令
.令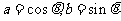 ,则
,则
 .因此 选
A.
.因此 选
A.
4.已知P为三角形ABC内部任一点(不包括边界),且满足 ,则△ABC一定为( )
,则△ABC一定为( )
A.直角三角形;B. 等边三角形;C. 等腰直角三角形;D. 等腰三角形
解:因为 ,所以已知条件可改写为
,所以已知条件可改写为 .容易得到此三角形为等腰三角形. 因此 选 D.
.容易得到此三角形为等腰三角形. 因此 选 D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com