
6.下列说法正确的是:
A.棉花属于天然有机高分子材料
B.缺铁会引起贫血,故人体补铁越多越好
C.多吃水果和蔬菜能给人体补充油脂
D.霉变的大米用清水洗干净后继续食用
5.下列有关水的说法正确的是:
A.蒸馏水属于硬水 B.净化水时,可用活性炭作杀菌剂
C.水变成水蒸气,水分子变大 D.湿衣服晾干说明分子作不断运动
4.下列说法正确的是:
A.木柴温度达到着火点就燃烧 B.化学反应中,原子都失去最外层电子
C.化学反应都伴有能量变化 D.催化剂在反应后质量会减少
3.下列变化属于化学变化的是:
A.干冰升华 B.电解水制氢气和氧气
C.汽油挥发 D.海水通过高分子分离膜制淡水
2.下列说法正确的是:
A.空气是混合物,其中氧气质量约占空气质量的五分之一
B.O2能跟所有物质发生氧化反应
C.CO和C都具有还原性,可用于冶金工业
D.香烟的烟气中含有二氧化碳等多种有毒物质
1.下列做法会加剧温室效应的是:
A.大力植树造林 B.鼓励私人使用小汽车代替公交车
C.骑自行车上下班 D.大量利用太阳能、风能和氢能等新能源
17. 将3k(k为正整数)个石子分成五堆.如果通过每次从其中3堆中各取走一个石子,而最后取完,则称这样的分法是“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
解: 分法是和谐的 充分必要条件 是 最多一堆石子的个数不超过k.………(5分)
下面设五堆石子的个数分别为a,b,c,d,e(其中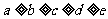 ).
).
“必要性”的证明: 若分法是和谐的,则把a所对应的石子取完至少要取a次,这a次每次都要取走3个石子.如果 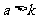 ,则
,则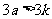 ,即把a所对应的一堆取完时,需取走的石子多于五堆石子的总数.矛盾.因此最多一堆石子的个数不能超过k.…………………(15分)
,即把a所对应的一堆取完时,需取走的石子多于五堆石子的总数.矛盾.因此最多一堆石子的个数不能超过k.…………………(15分)
“充分性”的证明:(数学归纳法)
(1) 当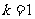 时,满足“
时,满足“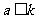 ” 的分法只能是1,1,1,0,0.显然这样的分法是和谐的.
” 的分法只能是1,1,1,0,0.显然这样的分法是和谐的.
(2) 假设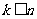 时,满足“
时,满足“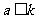 ” 的分法是和谐的.
” 的分法是和谐的.
(3) 当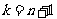 时,若
时,若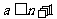 ,且分法a,b,c,d,e是不和谐的,则分法a-1,b-1,c-1, d, e也是不和谐的.由(2)及必要性的证明,可知
,且分法a,b,c,d,e是不和谐的,则分法a-1,b-1,c-1, d, e也是不和谐的.由(2)及必要性的证明,可知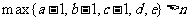 .
.
因为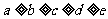 ,所以
,所以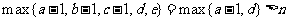 .
.
若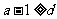 ,则有
,则有 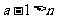 .这与
.这与 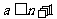 矛盾.
矛盾.
若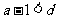 ,则有
,则有 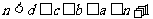 ,从而有
,从而有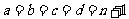 ,于是有
,于是有
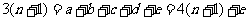 ,这是不可能的.矛盾.
,这是不可能的.矛盾.
因此当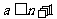 时,分法a,b,c,d,e是和谐的.…………………………………………(25分)
时,分法a,b,c,d,e是和谐的.…………………………………………(25分)
16.设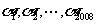 为2008个整数,且
为2008个整数,且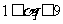 (
(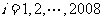 ).如果存在某个
).如果存在某个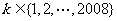 ,使得2008位数
,使得2008位数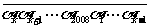 被101整除,试证明:对一切
被101整除,试证明:对一切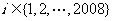 ,2008位数
,2008位数 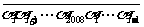 均能被101整除.
均能被101整除.
解: 根据已知条件,不妨设k=1,即2008位数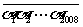 被101整除,只要能证明2008位数
被101整除,只要能证明2008位数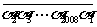 能被101整除. ……………………(5分)
能被101整除. ……………………(5分)
事实上,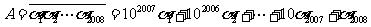 ,
,
 ……………………(10分)
……………………(10分)
从而有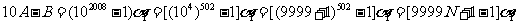 ,
,
即有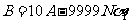 .……………………(20分)
.……………………(20分)
因为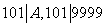 ,所以
,所以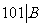 . 利用上述方法依次类推可以得到
. 利用上述方法依次类推可以得到
对一切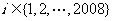 ,2008位数
,2008位数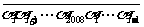 均能被101整除.……(25分)
均能被101整除.……(25分)
15.设非负等差数列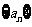 的公差
的公差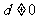 ,记
,记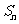 为数列
为数列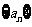 的前n项和,证明:
的前n项和,证明:
(1)若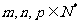 ,且
,且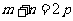 ,则
,则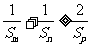 ;
;
(2)若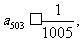 则
则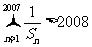 。
。
解:设非负等差数列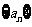 的首项为
的首项为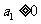 ,公差为
,公差为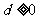 .
.
(1)因为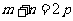 ,所以
,所以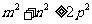 ,
,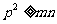 ,
,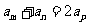 .
.
从而有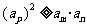 . 因为
. 因为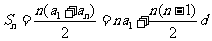 ,所以有
,所以有
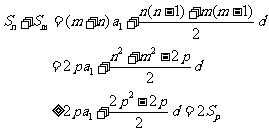 ……………………(5分)
……………………(5分)

于是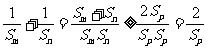 . ……………………(10分)
. ……………………(10分)
(2) 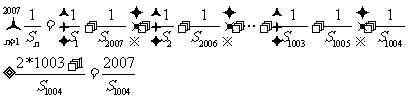 ………(15分)
………(15分)
又因为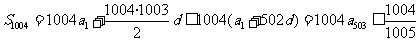 ,所以有
,所以有
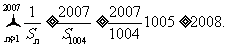 …………………………………………(20分)
…………………………………………(20分)
14.求解不等式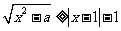 。
。
解:(I)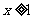 情形.此时不等式为
情形.此时不等式为 .于是有
.于是有
(1) .
.
因此 当 时,有
时,有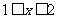 ;当
;当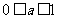 时,有
时,有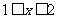 ;
;
当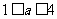 时,有
时,有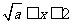 ;当
;当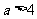 时,空集. …………………… (5分)
时,空集. …………………… (5分)
(2)  .
.
此时有 当 时,有
时,有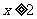 ;当
;当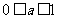 时,有
时,有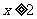 ;当
;当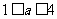 时,有
时,有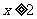 ;当
;当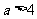 时,
时,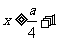 .
…………………………………………(10分)
.
…………………………………………(10分)
(II)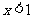 情形.此时不等式为
情形.此时不等式为 .
.
于是有
(3) .
.
因此 当 时,有
时,有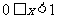 ;当
;当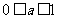 时,有
时,有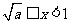 ;当
;当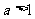 时,空集.……(15分)
时,空集.……(15分)
(4) .
.
因此 当 时,有
时,有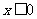 ;当
;当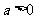 时,空集.
时,空集.
综合(1)-(4)可得
当 时,有
时,有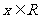 ;当
;当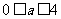 时,有
时,有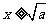 ;当
;当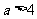 时,
时,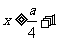 .…(20分)
.…(20分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com