
22.已知直线l与抛物线 相切于点
相切于点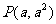 ,又与抛物线
,又与抛物线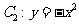 相交于两点A、B. 分别过A、B作
相交于两点A、B. 分别过A、B作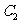 的切线
的切线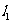 ,
,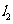 相交于点Q,设
相交于点Q,设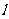 ,
,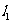 ,
,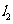 的斜率分别为
的斜率分别为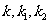 .
.
求证:(Ⅰ)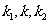 成等差数列;
成等差数列;
(Ⅱ)点Q在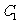 上.
上.
证明:(Ⅰ)设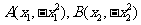 ,
,
对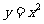 求导得
求导得 ;
;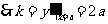 ,
,
所以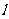 的方程为
的方程为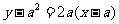 ,即
,即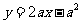 ,代入
,代入 得
得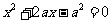 ,
,
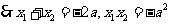 .
.
对 求导得
求导得 ;
;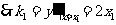 ,
, ;
;
从而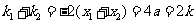 ,
,
所以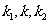 成等差数列;
成等差数列;
(Ⅱ)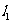 的方程为
的方程为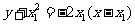 ,即
,即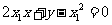 ,
,
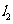 的方程为
的方程为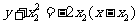 ,即
,即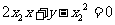 ,
,
两式相减得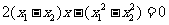 ,
,
即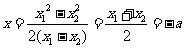 ,
,
将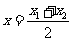 代入
代入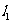 的方程得
的方程得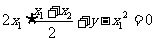 ,
,
即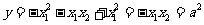 ,
,
所以点Q的坐标为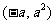 ,显然满足
,显然满足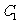 的方程,
的方程,
故点Q在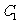 上.
上.
21.  的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数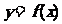 的单调区间;
的单调区间;
(Ⅱ)若a>0,求函数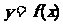 在区间(a -1,a+1)内的极值..
在区间(a -1,a+1)内的极值..
解:(Ⅰ)由函数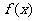 图象过点(-1,-6),得
图象过点(-1,-6),得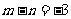 ,①
,①
由 ,得
,得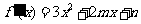 ,
,
则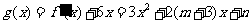 ;
;
而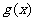 图象关于y轴对称,
图象关于y轴对称,
所以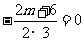 ,所以
,所以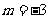 , 代入①得
, 代入①得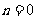 .
.
于是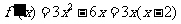 .
.
由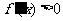 得
得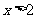 或
或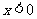 ,
,
故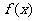 的单调递增区间是(-∞,0),(2,+∞);
的单调递增区间是(-∞,0),(2,+∞);
由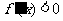 得
得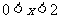 ,
,
故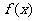 的单调递减区间是(0,2).
的单调递减区间是(0,2).
(Ⅱ)由(Ⅰ)得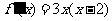 ,
,
令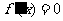 得
得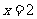 或
或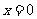 .
.
当x变化时,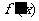 、
、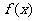 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞.0) |
0 |
(0,2) |
2 |
(2,+ ∞) |
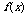 |
+ |
0 |
- |
0 |
+ |
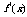 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得:
当0<a<1时,f(x)有极大值-2,无极小值,
当1<a<3时,f(x)有极小值-6,无极大值;
当a=1或a≥3时,f(x)无极值.
20.如图,一张平行四边形的硬纸片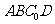 中,
中,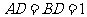 ,
,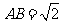 .沿它的对角线
.沿它的对角线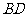 把
把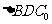 折起,使点
折起,使点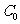 到达平面
到达平面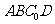 外点
外点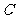 的位置.
的位置.
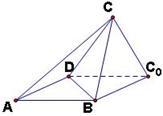 (Ⅰ)证明:平面
(Ⅰ)证明:平面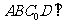 平面
平面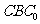 ;
;
(Ⅱ)如果△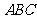 为等腰三角形,求二面角
为等腰三角形,求二面角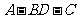 的大小。
的大小。
解:(Ⅰ)证明:因为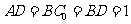 ,
,
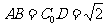 ,所以
,所以 .
.
因为折叠过程中, ,
,
所以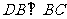 ,又
,又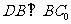 ,故
,故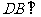 平面
平面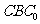 .
.
又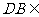 平面
平面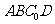 ,
,
所以平面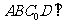 平面
平面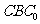 .
.
(Ⅱ)解法一:如图,延长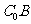 到
到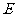 ,使
,使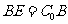 ,连结
,连结 ,
,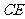 。
。
因为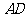

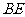 ,
,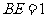 ,
,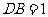 ,
,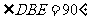 ,所以
,所以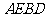 为正方形,
为正方形,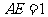 。
。
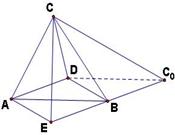 由于
由于 ,
,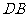 都与平面
都与平面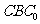 垂直,所以
垂直,所以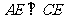 ,可知
,可知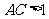 。
。
因此只有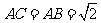 时,△
时,△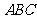 为等腰三角形。
为等腰三角形。
在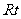 △
△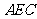 中,
中,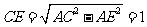 ,又
,又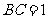 ,
,
所以△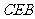 为等边三角形,
为等边三角形,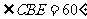 。
。
由(Ⅰ)可知,,所以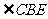 为二面角
为二面角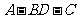 的平面角,即二面角
的平面角,即二面角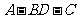 的大小为
的大小为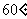 。
。
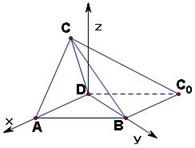
解法二:以 为坐标原点,射线
为坐标原点,射线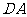 ,
,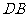 分别为
分别为 轴正半轴和
轴正半轴和 轴正半轴,建立如图的空间直角坐标系
轴正半轴,建立如图的空间直角坐标系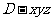 ,则
,则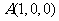 ,
,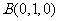 ,
,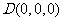 。
。
 由(Ⅰ)可设点
由(Ⅰ)可设点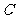 的坐标为
的坐标为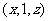 ,其中
,其中 ,则有
,则有 。 ①
。 ①
因为△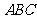 为等腰三角形,所以
为等腰三角形,所以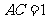 或
或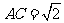 。
。
若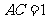 ,则有
,则有 。
。
则此得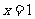 ,
,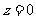 ,不合题意。
,不合题意。
若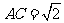 ,则有
,则有 。
②
。
②
联立①和②得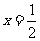 ,
,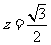 。故点
。故点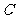 的坐标为
的坐标为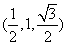 。
。
由于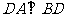 ,
,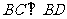 ,所以
,所以 与
与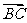 夹角的大小等于二面角
夹角的大小等于二面角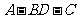 的大小。
的大小。
又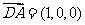 ,
,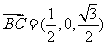 ,
,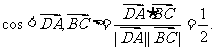
所以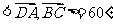 即二面角
即二面角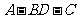 的大小为
的大小为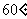 。
。
18. 已知函数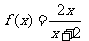 ,定义数列
,定义数列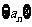 ,使:
,使: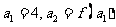 ,…,
,…,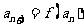 … .
… .
(1)求证:数列 是等差数列;
是等差数列;
(2)设数列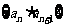 的前n项和为
的前n项和为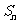 ,求
,求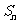 .
.
解:(1)∵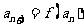 ∴
∴
∴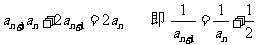
又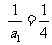 ∴数列{
∴数列{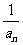 }是以
}是以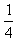 为首项,以
为首项,以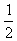 为公差的等差数列.
为公差的等差数列.
(2)由(1)可知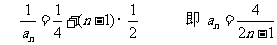
∴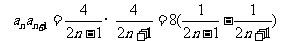
∴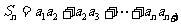
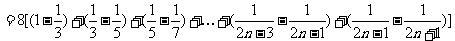
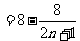 .
.
19:已知
(1)若p > 1时,解关于x的不等式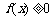 ;
;
(2)若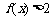 对
对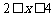 时恒成立,求p的范围..
时恒成立,求p的范围..
解:(1) 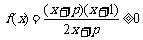
①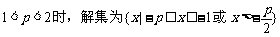
② p = 2时,解集为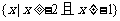
③ p > 2时,解集为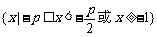
(2) 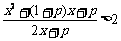
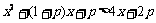
∴ 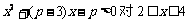 恒成立
恒成立
∴ 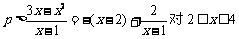 恒成立
恒成立
∵  上递减
上递减
∴ 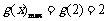
∴ p > 2.
17.已知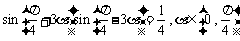 ,求
,求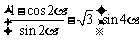 的值.
的值.
解: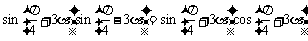
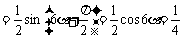 ,
,
即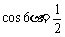 ,又∵
,又∵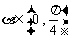 ,∴
,∴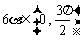
∴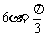 ,即
,即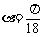 .
.
∴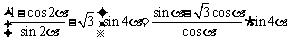
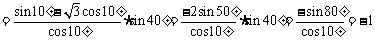
16、正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
①点E到平面ABC1D1的距离为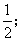
②直线BC与平面ABC1D1所成的角等于45°;
③空间四边形ABCD1在正方体六个面内形成六个射影,其面积的最小值是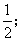
④AE与DC1所成的角为 ;
;
⑤二面角A-BD1-C的大小为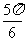 .
.
其中真命题是 .(写出所有真命题的序号)(②③④)
15、点P是离心率为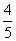 ,左、右焦点分别为
,左、右焦点分别为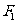 和
和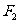 的椭圆上一点,且
的椭圆上一点,且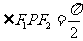 ,
,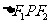 的面积为
的面积为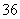 ,则椭圆的方程是
.答案:
,则椭圆的方程是
.答案: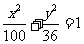 .
.
14、函数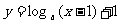
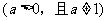 的图象恒过定点
的图象恒过定点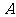 ,若点
,若点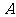 在一次函数
在一次函数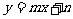 的图象上,其中
的图象上,其中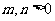 ,则
,则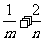 的最小值为_ .答案:
的最小值为_ .答案: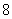
13、设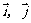 是平面直角坐标系(坐标原点为
是平面直角坐标系(坐标原点为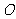 )内分别与
)内分别与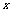 轴、
轴、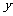 轴正方向相同的两个单位向量,且
轴正方向相同的两个单位向量,且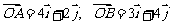 ,则
,则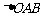 的面积等于
.答案:5
的面积等于
.答案:5
12、正四面体ABCD的棱长为1,棱AB//平面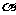 ,则正四面体上的所有点在平面
,则正四面体上的所有点在平面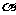 内的射影构成图形面积的取值范围是(
)
内的射影构成图形面积的取值范围是(
)
A、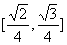 B、
B、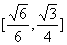 C、
C、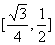 D、
D、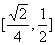
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com