
例7.已知a>0且a≠1,试求使方程log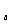 (x-ak)=log
(x-ak)=log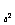 (x
(x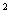 -a
-a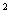 )
)
有解的实数k的取值范围。
解:原方程等价于0<x-ak=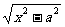
构造曲线C:y= ,直线L:y= x-ak
,直线L:y= x-ak
 从而使问题转化为直线L和双曲线C:x
从而使问题转化为直线L和双曲线C:x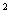 -y
-y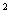 =a
=a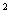 (y≥0)x轴上半部分有交点,求实数k的取值范围,如图所示:
(y≥0)x轴上半部分有交点,求实数k的取值范围,如图所示:
有三条临界直线L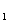 、L
、L 、L
、L
①
当L在L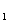 和L
和L 之间时,直线L在y轴上的截距
之间时,直线L在y轴上的截距
② -ak满足-a<-ak<0时L与C有一个交点,
解之可得0<k<1
③ 当L在L 上方时,直线L在y轴上的截距-ak满
上方时,直线L在y轴上的截距-ak满
足a<-ak时L与C有一个交点,
解之可得k<-1
综合①②可得,所求k的取值范围是
 例8.求函数y=
例8.求函数y= +
+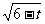 的值域。
的值域。
解:设m= , n=
, n=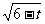 , 则m
, 则m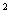 +n
+n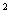 =16 (0≤m≤4,0≤n≤2
=16 (0≤m≤4,0≤n≤2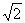 )
)
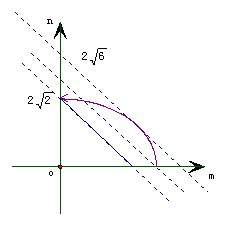
原函数可变形为y=m+n, y表示直线在n轴上的截距,结合图形可知
y =2
=2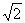 , y
, y =2
=2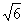
点评:这两道题目可以建立目标函数,然后利用求函数最值的方法解决,但利用圆锥曲线定义数形结合求解,事半功倍,迅速而准确。
例6.已知sin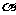 +sin
+sin =
= , cos
, cos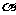 +cos
+cos =
= , 求tan(
, 求tan(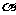 +
+ )的值
)的值
 解:点A(cos
解:点A(cos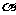 ,sin
,sin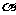 )B(cos
)B(cos ,sin
,sin )
)
都在单位圆上,由已知可知A和B的中点C坐标
(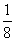 ,
, ),则直线AB过定点C
),则直线AB过定点C
∠xOC= 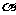 +
+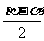 =
=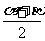
∴tan∠xOC= tan 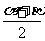 =
=
∴tan( +
+ )=
)= =
=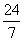
点评:另外,单位圆中的三角函数线可以辅助解决三角不等式(组)问题。
求含有两个变量的线性式子的最值,可以构造直线方程,利用截距的意义解决问题。这一应用在线性规划中体现的很充分---求线性目标函数的最值。
例5.已知x,y满足条件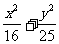 =1,求y-3x的最小值和最大值
=1,求y-3x的最小值和最大值
解:令y-3x=b, 即y=3x+b
由 联立可得: 169
联立可得: 169 +966y
+966y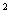 +16b
+16b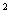 -400=0,令⊿≥0得:
-400=0,令⊿≥0得:
-13≤b≤13
∴y-3x的最小值和最大值分别是-13和13。
 求通过变形可以出现
求通过变形可以出现 的模式的式子的最值问题,可以优先考虑两点间的距离公式的利用
的模式的式子的最值问题,可以优先考虑两点间的距离公式的利用
例4.函数y= 的最小值为
。
的最小值为
。
解析:函数可化为y= -
-
这个式子表示P(x,0)到点A(6,4)和点B(2,1)的差,
由右图可知,当P、A、B三点共线时,
︱PA︱-︱PB︱≤︱AB︱, ︱AB︱=5
函数取得最大值为5
提示:a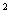 +b
+b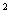 =(
=( )
)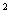 =(
=( )
)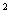 ,表示点(a,b)到原点的距离。
,表示点(a,b)到原点的距离。
分式型的最值问题可以通过变形,利用斜率公式解决。
例3.函数y= 最大值是
,最小值是
。
最大值是
,最小值是
。
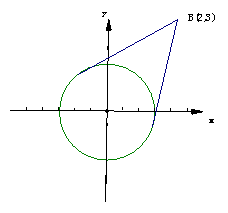 解:函数解析式表示经过A(-cosx,sinx)和B(2,3)两点连线的斜率k,A在单位圆x
解:函数解析式表示经过A(-cosx,sinx)和B(2,3)两点连线的斜率k,A在单位圆x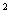 +y
+y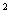 =1上,经过A和B两点的直线方程为y-3=k(x-2)
=1上,经过A和B两点的直线方程为y-3=k(x-2)
即kx-y+3-2k=0,由直线和圆的位置关系得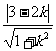 ≤1解之可得;
≤1解之可得; 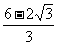 ≤k≤
≤k≤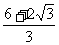
所以函数得最大值是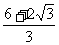 最小值是
最小值是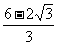 。
。
例1.(1)(2003上海春,5)已知集合A={x||x|≤2,x∈R},B={x|x≥a},且A B,则实数a的取值范围是_____.
B,则实数a的取值范围是_____.
解析:(1)a≤-2;
 ∵A={x|-2≤x≤2},B={x|x≥a},又A
∵A={x|-2≤x≤2},B={x|x≥a},又A B,利用数轴上覆盖关系,
B,利用数轴上覆盖关系,
因此有a≤-2.
点评:利用韦恩图和数轴可以直观地解决集合问题
韦恩图是解决集合运算问题常用的工具,还可证明一些常用的恒等式,如A∩B=A∪B A=B,A=A∩B
A=B,A=A∩B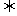 A
A B
B B=A∪B,C
B=A∪B,C (A∩B)= C
(A∩B)= C A∪C
A∪C B, C
B, C (A∪B)= C
(A∪B)= C A∩C
A∩C B等。
B等。
例1.某班50人中,参见数学竞赛的25人,参加化学竞赛的32人,求既参加数学竞赛又参加化学竞赛的人数的最大值和最小值。
解:设两科都参加的人数是x人,则参加化学竞赛和参加数学竞赛的人数分别是32-x,25-x
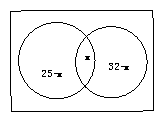 根据题意的实际意义得:
根据题意的实际意义得: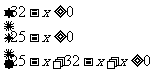 ,解不等式可得
,解不等式可得
7≤x≤25
∴两科都参加得人数的最大值是25和最小值是7
29. (12分) 某实验小组用通过右图装置合成乙酸乙酯。在图中蒸馏烧瓶A内加入乙醇、浓硫酸和无水乙酸,加热一段时间后即可在锥形瓶内得到乙酸乙酯粗产品。
(12分) 某实验小组用通过右图装置合成乙酸乙酯。在图中蒸馏烧瓶A内加入乙醇、浓硫酸和无水乙酸,加热一段时间后即可在锥形瓶内得到乙酸乙酯粗产品。
请回答下列问题:
(1) 在蒸馏烧瓶A中除加入乙醇、浓硫酸和无水乙酸外,还应放入碎瓷片,其目的是 。蒸馏烧瓶A中发生的反应的化学方程式为 。
(2)收集产品时,不使用玻璃导管,而使用仪器B的原因是 。
(3)实验中加热保持沸腾的主要目的有 , 。
(4)锥形瓶内收集的乙酸乙酯粗产品中所含杂质主要有 。
现拟通过以下操作步骤从所得粗产品中分离出各成分。(分离后允许含有少量水)。

操作一的名称是 ,在C中加入的试剂a是 ,
操作三的名称是 。进行操作二后所得的E物质是 。



28.(12分) A~I 九种有机物的转化关系如图所示。

3. 
(1) A的结构简式为 。
(2) ①E→F反应的化学方程式为: 。
②C4H8O2与热的NaOH溶液反应的化学方程式为: 。
(3) 在一定条件下,由F经一步或若干步可合成六元环X。若X的分子式为C4H8O2,则F的结构简式为 ;若X的分子式为C4H4O4,则最后一步反应的化学方程式为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com