
5.甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为 。
。
Ⅰ.分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
Ⅱ.从甲、乙、丙加工的零件中各取一个进行检验,求至少有一个是一等品的概率。
4.已知锐角三角形ABC中, 。
。
Ⅰ.求证 ;
;
Ⅱ.设 ,求AB边上的高。
,求AB边上的高。
3.设双曲线的焦点 在轴上,两条渐近线为
在轴上,两条渐近线为 ,则该双曲线的离心率
,则该双曲线的离心率 ( )
( )
A 5
B  C
C  D
D 
2.已知方程 的四个根组成一个首项为
的四个根组成一个首项为 的等差数列,则
的等差数列,则 (
)
(
)
A 1
B  C
C  D
D 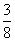
1.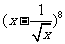 展开式中
展开式中 的系数为____________.
的系数为____________.
Ⅰ.运用函数与方程、表达式相互转化的观点解决函数、方程、表达式问题。
例1 已知 ,(a、b、c∈R),则有( )
,(a、b、c∈R),则有( )
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
解析 法一:依题设有 a·5-b· +c=0
+c=0
∴ 是实系数一元二次方程
是实系数一元二次方程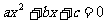 的一个实根;
的一个实根;
∴△=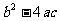 ≥0 ∴
≥0 ∴ 故选(B)
故选(B)
法二:去分母,移项,两边平方得:
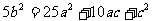 ≥10ac+2·5a·c=20ac
≥10ac+2·5a·c=20ac
∴ 故选(B)
故选(B)
点评解法一通过简单转化,敏锐地抓住了数与式的特点,运用方程的思想使问题得到解决;解法二转化为b2是a、c的函数,运用重要不等式,思路清晰,水到渠成。
练习1 已知关于 的方程
的方程  -(2 m-8)x +
-(2 m-8)x + -16 = 0的两个实根
-16 = 0的两个实根  、
、 满足
满足  <
< <
< ,则实数m的取值范围_______________。
,则实数m的取值范围_______________。
答案: ;
;
 2 已知函数
2 已知函数  的图象如下,则( )
的图象如下,则( )
(A) (B)
(B)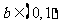
(C) 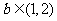 (D)
(D)
答案:A.
3 求使不等式 ≤
≤ ·
· 对大于1的任意x、y恒成立的a的取值范围。
对大于1的任意x、y恒成立的a的取值范围。
Ⅱ:构造函数或方程解决有关问题:
例2 已知 ,t∈[
,t∈[ ,8],对于f(t)值域内的所有实数m,不等式
,8],对于f(t)值域内的所有实数m,不等式 恒成立,求x的取值范围。
恒成立,求x的取值范围。
解析∵t∈[ ,8],∴f(t)∈[
,8],∴f(t)∈[ ,3]
,3]
原题转化为: >0恒成立,为m的一次函数(这里思维的转化很重要)
>0恒成立,为m的一次函数(这里思维的转化很重要)
当x=2时,不等式不成立。
∴x≠2。令g(m)= ,m∈[
,m∈[ ,3]
,3]
问题转化为g(m)在m∈[ ,3]上恒对于0,则:
,3]上恒对于0,则: ;
;
解得:x>2或x<-1
评析 首先明确本题是求x的取值范围,这里注意另一个变量m,不等式的左边恰是m的一次函数,因此依据一次函数的特性得到解决。在多个字母变量的问题中,选准“主元”往往是解题的关键。
例3 为了更好的了解鲸的生活习性,某动物保护组织在受伤的鲸身上装了电子监测装置,从海洋放归点A处,如图(1)所示,把它放回大海,并沿海岸线由西向东不停地对它进行了长达40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动),然后又在观测站B处对鲸进行生活习性的详细观测,已知AB=15km,观测站B的观测半径为5km。
|
观测时刻 t(分钟) |
跟踪观测点到放归 点的距离a(km) |
鲸位于跟踪观测点正北 方向的距离b(km) 方向的距离b(km) |
|
10 |
1 |
0.999 |
|
20 |
2 |
1.413 |
|
30 |
3 |
1.732 |
|
40 |
4 |
2.001 |
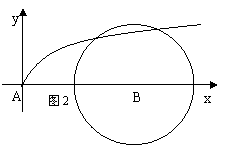
(1)据表中信息:①计算出鲸沿海岸线方向运动的速度;②试写出a、b近似地满足的关系式并
画出鲸的运动路线草图;
 (2)若鲸继续以(1)-②运动的路线运动,试预测,该鲸经过多长时间(从放归时开设计时)可进入前方观测站B的观测范围?并求出可持续观测的时间及最佳观测时刻。(注:
(2)若鲸继续以(1)-②运动的路线运动,试预测,该鲸经过多长时间(从放归时开设计时)可进入前方观测站B的观测范围?并求出可持续观测的时间及最佳观测时刻。(注: ≈6.40;精确到1分钟)
≈6.40;精确到1分钟)
解析(1)由表中的信息可知:
①鲸沿海岸线方向运动的速度为: (km/分钟)
(km/分钟)
②a、b近似地满足的关系式为: 运动路线如图
运动路线如图
(2)以A为原点,海岸线AB为x轴建立直角坐标系,设鲸所在
位置点P(x,y),由①、②得: ,又B(15,0),
,又B(15,0),
依题意:观测站B的观测范围是:
 ≤5 (y≥0) 又
≤5 (y≥0) 又
∴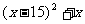 ≤25 解得:11.30≤x≤17.70
≤25 解得:11.30≤x≤17.70
由①得:∴该鲸经过t= =113分钟可进入前方观测站B的观测范围
=113分钟可进入前方观测站B的观测范围
持续时间: =64分钟
=64分钟
∴该鲸与B站的距离d= =
=
当d最小时为最佳观测时刻,这时x= =14.5,t=145分钟。
=14.5,t=145分钟。
练习4.已知关于 的方程
的方程 -2
-2 = 0有实数解,求实数
= 0有实数解,求实数 的取值范围。
的取值范围。
(答案:0≤ ≤4-
≤4- )
)
Ⅲ:运用函数与方程的思想解决数列问题
例4设等差数列{an}的前n项和为Sn,已知 ,
,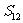 >0,
>0, <0,
<0,
(1)求公差d的取值范围;
(2)指出 、
、 、
、 …,
…,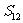 中哪一个最大,并说明理由。
中哪一个最大,并说明理由。
解析(1)由 得:
得: ,
,
∵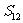 =
= >0
>0  =
= <0
<0
∴ <d<-3
<d<-3
(2)
∵d<0,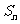 是关于n 的二次函数,对称轴方程为:x=
是关于n 的二次函数,对称轴方程为:x=
∵ <d<-3 ∴6<
<d<-3 ∴6< <
< ∴当n=6时,
∴当n=6时,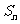 最大。
最大。
3.(1) 函数和方程是密切相关的,对于函数y=f(x),当y=0时,就转化为方程f(x)=0,也可以把函数式y=f(x)看做二元方程y-f(x)=0。函数问题(例如求反函数,求函数的值域等)可以转化为方程问题来求解,方程问题也可以转化为函数问题来求解,如解方程f(x)=0,就是求函数y=f(x)的零点。
(2) 函数与不等式也可以相互转化,对于函数y=f(x),当y>0时,就转化为不等式f(x)>0,借助于函数图像与性质解决有关问题,而研究函数的性质,也离不开解不等式。
(3) 数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列问题十分重要。
(4) 函数f(x)= (n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。
(n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。
(5) 解析几何中的许多问题,例如直线和二次曲线的位置关系问题,需要通过解二元方程组才能解决,涉及到二次方程与二次函数的有关理论。
(6) 立体几何中有关线段、角、面积、体积的计算,经常需要运用布列方程或建立函数表达式的方法加以解决。
2.方程的思想,就是分析数学问题中变量间的等量关系,建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。方程的数学是对方程概念的本质认识,用于指导解题就是善于利用方程或方程组的观点观察处理问题。方程思想是动中求静,研究运动中的等量关系.
函数与方程是两个不同的概念,但它们之间有着密切的联系,方程f(x)=0的解就是函数y=f(x)的图像与x轴的交点的横坐标,函数y=f(x)也可以看作二元方程f(x)-y=0通过方程进行研究。
就中学数学而言,函数思想在解题中的应用主要表现在两个方面:一是借助有关初等函数的性质,解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题:二是在问题的研究中,通过建立函数关系式或构造中间函数,把所研究的问题转化为讨论函数的有关性质,达到化难为易,化繁为简的目的.许多有关方程的问题可以用函数的方法解决,反之,许多函数问题也可以用方程的方法来解决。函数与方程的思想是中学数学的基本思想,也是历年高考的重点。
1.函数的思想,是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决。函数思想是对函数概念的本质认识,用于指导解题就是善于利用函数知识或函数观点观察、分析和解决问题。
“三化”:(1)问题具体化(包括抽象函数用具有相同性质的具体函数作为代表来研究,字母用常数来代表)。即把题目中所涉及的各种概念或概念之间的关系具体明确,有时可画表格或图形,以便于把一般原理、一般规律应用到具体的解题过程中去。(2)问题简单化。即把综合问题分解为与各相关知识相联系的简单问题,把复杂的形式转化为简单的形式。(3)问题和谐化。即强调变换问题的条件或结论,使其表现形式符合数或形内部固有的和谐统一的特点,或者突出所涉及的各种数学对象之间的知识联系。
“三转”:(1)语言转换能力。每个数学综合题都是由一些特定的文字语言、符号语言、图形语言所组成。解综合题往往需要较强的语言转换能力。还需要有把普通语言转换成数学语言的能力。(2)概念转换能力:综合题的转译常常需要较强的数学概念的转换能力。(3)数形转换能力。解题中的数形结合,就是对题目的条件和结论既分析其代数含义又分析其几何意义,力图在代数与几何的结合上找出解题思路。运用数形转换策略要注意特殊性,否则解题会出现漏洞。
“三思”:(1)思路:由于综合题具有知识容量大,解题方法多,因此,审题时应考虑多种解题思路。(2)思想:高考综合题的设置往往会突显考查数学思想方法,解题时应注意数学思想方法的运用。(3)思辩:即在解综合题时注意思路的选择和运算方法的选择。
“三联”:(1)联系相关知识,(2)连接相似问题,(2)联想类似方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com