
5.如果函数f(x)=x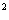 +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
A. f(2)<f(1)<f(4) B. f(1)<f(2)<f(4)
C. f(2)<f(4)<f(1) D. f(4)<f(2)<f(1)
4.方程lgx+x=3的解所在的区间为 ( )
A. (0,1) B. (1,2) C. (2,3) D. (3,+∞)
3.已知命题p:函数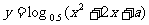 的值域为R,命题q:函数
的值域为R,命题q:函数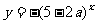
是减函数。若p或q为真命题,p且q为假命题,则实数a的取值范围是
A.a≤1 B.a<2 C.1<a<2 D.a≤1或a≥2
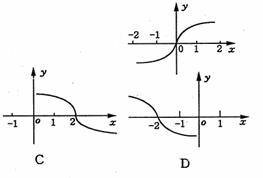
2.方程f(x,y)=0的曲线如图所示,那么方程f(2-x,y)=0的曲线是 ( )
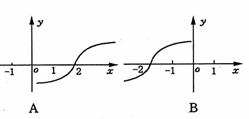
1.对函数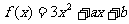 作代换x=g(t),则总不改变f(x)值域的代换是 ( ) A.
作代换x=g(t),则总不改变f(x)值域的代换是 ( ) A.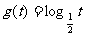 B.
B.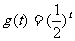
C.g(t)=(t-1)2 D.g(t)=cost
2.掌握研究函数的方法,提高研究函数问题的能力
高中数学对函数的研究理论性加强了,对一些典型问题的研究十分重视,如求函数的定义域,确定函数的解析式,判断函数的奇偶性,判断或证明函数在指定区间的单调性等,并形成了研究这些问题的初等方法,这些方法对分析问题能力,推理论证能力和综合运用数学知识能力的培养和发展是十分重要的.
函数、方程、不等式是相互联系的.对于函数f(x)与g(x),令f(x)=g(x),f(x)>g(x)或f(x)<g(x)则分别构成方程和不等式,因此对于某些方程、不等式的问题用函数观点认识是十分有益的;方程、不等式从另一个侧面为研究函数提供了工具.
例10.方程lgx+x=3的解所在区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
分析:在同一平面直角坐标系中,画出函数y=lgx与y=-x+3的图象(如图2).它们的交点横坐标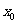 ,显然在区间(1,3)内,由此可排除A,D.至于选B还是选C,由于画图精确性的限制,单凭直观就比较困难了.实际上这是要比较
,显然在区间(1,3)内,由此可排除A,D.至于选B还是选C,由于画图精确性的限制,单凭直观就比较困难了.实际上这是要比较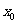 与2的大小.当x=2时,lgx=lg2,3-x=1.由于lg2<1,因此
与2的大小.当x=2时,lgx=lg2,3-x=1.由于lg2<1,因此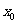 >2,从而判定
>2,从而判定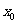 ∈(2,3),故本题应选C.
∈(2,3),故本题应选C.
说明:本题是通过构造函数用数形结合法求方程lgx+x=3解所在的区间.数形结合,要在结合方面下功夫.不仅要通过图象直观估计,而且还要计算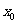 的邻近两个函数值,通过比较其大小进行判断.
的邻近两个函数值,通过比较其大小进行判断.
例11.(1)一次函数f(x)=kx+h(k≠0),若m<n有f(m)>0,f(n)>0,则对于任意x∈(m,n)都有f(x)>0,试证明之;
(2)试用上面结论证明下面的命题:
若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
分析:问题(1)实质上是要证明,一次函数f(x)=kx+h(k≠0), x∈(m, n).若区间两个端点的函数值均为正,则对于任意x∈(m,n)都有f(x)>0.之所以具有上述性质是由于一次函数是单调的.因此本问题的证明要从函数单调性入手.
(1)证明:
当k>0时,函数f(x)=kx+h在x∈R上是增函数,m<x<n,f(x)>f(m)>0;
当k<0时,函数f(x)=kx+h在x∈R上是减函数,m<x<n,f(x)>f(n)>0.
所以对于任意x∈(m,n)都有f(x)>0成立.
(2)将ab+bc+ca+1写成(b+c)a+bc+1,构造函数f(x)=(b+c)x+bc+1.则
f(a)=(b+c)a+bc+1.
当b+c=0时,即b=-c, f(a)=bc+1=-c2+1.
因为|c|<1,所以f(a)=-c2+1>0.
当b+c≠0时,f(x)=(b+c)x+bc+1为x的一次函数.
因为|b|<1,|c|<1,
f(1)=b+c+bc+1=(1+b)(1+c)>0, f(-1)=-b-c+bc+1=(1-b)(1-c)>0.
由问题(1)对于|a|<1的一切值f(a)>0,即(b+c)a+bc+1=ab+ac+bc+1>0.
说明:问题(2)的关键在于“转化”“构造”.把证明ab+bc+ca>-1转化为证明ab+bc+ca+1>0, 由于式子ab+bc+ca+1中, a,b,c是对称的,构造函数f(x)=(b+c)x+bc+1,则f(a)=(b+c)a+bc+1,问题转化为在|a|<1,|b|<1,|c|<1的条件下证明f(a)>0.(也可构造 f(x)=(a+c)x+ac+1,证明f(b)>0)。
例12.定义在R上的单调函数f(x)满足f(3)=log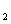 3且对任意x,y∈R都有f(x+y)=f(x)+f(y).
3且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3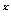 )+f(3
)+f(3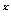 -9
-9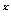 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
分析:欲证f(x)为奇函数即要证对任意x都有f(-x)=-f(x)成立.在式子f(x+y)=f(x)+f(y)中,令y=-x可得f(0)=f(x)+f(-x)于是又提出新的问题,求f(0)的值.令x=y=0可得f(0)=f(0)+f(0)即f(0)=0,f(x)是奇函数得到证明.
(1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.
(2)解:f(3)=log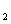 3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k·3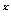 )<-f(3
)<-f(3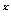 -9
-9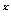 -2)=f(-3
-2)=f(-3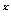 +9
+9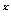 +2), k·3
+2), k·3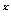 <-3
<-3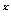 +9
+9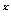 +2,
+2,
3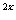 -(1+k)·3
-(1+k)·3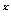 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3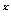 >0,问题等价于t
>0,问题等价于t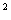 -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.
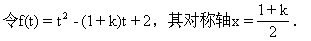
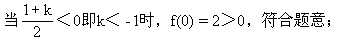

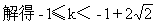
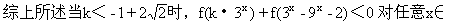 R恒成立.
R恒成立.
说明:问题(2)的上述解法是根据函数的性质.f(x)是奇函数且在x∈R上是增函数,把问题转化成二次函数f(t)=t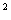 -(1+k)t+2对于任意t>0恒成立.对二次函数f(t)进行研究求解.本题还有更简捷的解法:
-(1+k)t+2对于任意t>0恒成立.对二次函数f(t)进行研究求解.本题还有更简捷的解法:
分离系数由k·3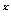 <-3
<-3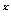 +9
+9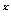 +2得
+2得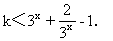
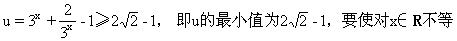
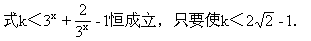
上述解法是将k分离出来,然后用平均值定理求解,简捷、新颖.
1.准确理解、熟练运用,不断深化有关函数的基础知识
在中学阶段函数只限于定义在实数集合上的一元单值函数,其内容可分为两部分.第一部分是函数的概念和性质,这部分的重点是能从变量的观点和集合映射的观点理解函数及其有关概念,掌握描述函数性质的单调性、奇偶性、周期性等概念;第二部分是七类常见函数(一次函数、二次函数、指数函数、对数函数、三角函数和反三角函数)的图象和性质.第一部分是理论基础,第二部分是第一部分的运用与发展.
例9.已知函数f(x),x∈F,那么集合{(x,y)|y=f(x),x∈F}∩{(x,y)|x=1}中所含元素的个数是.( )
A.0 B.1 C.0或1 D.1或2
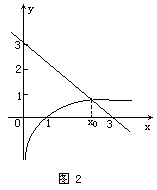 分析:这里首先要识别集合语言,并能正确把集合语言转化成熟悉的语言.从函数观点看,问题是求函数y=f(x),x∈F的图象与直线x=1的交点个数(这是一次数到形的转化),不少学生常误认为交点是1个,并说这是根据函数定义中“惟一确定”的规定得到的,这是不正确的,因为函数是由定义域、值域、对应法则三要素组成的.这里给出了函数y=f(x)的定义域是F,但未明确给出1与F的关系,当1∈F时有1个交点,当1
分析:这里首先要识别集合语言,并能正确把集合语言转化成熟悉的语言.从函数观点看,问题是求函数y=f(x),x∈F的图象与直线x=1的交点个数(这是一次数到形的转化),不少学生常误认为交点是1个,并说这是根据函数定义中“惟一确定”的规定得到的,这是不正确的,因为函数是由定义域、值域、对应法则三要素组成的.这里给出了函数y=f(x)的定义域是F,但未明确给出1与F的关系,当1∈F时有1个交点,当1 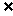 F时没有交点,所以选C.
F时没有交点,所以选C.
4.树立函数思想,使学生善于用运动变化的观点分析问题.
本部分内容的重点是:通过对问题的讲解与分析,使学生能较好的调动函数的基础知识解决问题,并在解决问题中深化对基础知识的理解,深化对函数思想、数形结合思想的理解与运用.
难点是:函数思想的理解与运用,推理论证能力、综合运用知识解决问题能力的培养与提高.
函数的综合运用主要是指运用函数的知识、思想和方法综合解决问题.函数描述了自然界中量的依存关系,是对问题本身的数量本质特征和制约关系的一种刻画,用联系和变化的观点提出数学对象,抽象其数学特征,建立函数关系.因此,运动变化、相互联系、相互制约是函数思想的精髓,掌握有关函数知识是运用函数思想的前提,提高用初等数学思想方法研究函数的能力,树立运用函数思想解决有关数学问题的意识是运用函数思想的关键.
3.初步沟通函数与方程、不等式及解析几何有关知识的横向联系,提高综合运用知识解决问题的能力.
2.掌握初等数学研究函数的方法,提高研究函数的能力,重视数形结合数学思想方法的运用和推理论证能力的培养.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com