
4.证明不等式的方法灵活多样,但比较法、综合法、分析法仍是证明不等式的最基本方法.要依据题设、题断的结构特点、内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤,技巧和语言特点.比较法的一般步骤是:作差(商)→变形→判断符号(值).
3.在不等式的求解中,换元法和图解法是常用的技巧之一,通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数,将不等式的解化归为直观、形象的图象关系,对含有参数的不等式,运用图解法,可以使分类标准更加明晰.
2.整式不等式(主要是一次、二次不等式)的解法是解不等式的基础,利用不等式的性质及函数的单调性,将分式不等式、绝对值不等式等化归为整式不等式(组)是解不等式的基本思想,分类、换元、数形结合是解不等式的常用方法.方程的根、函数的性质和图象都与不等式的解密切相关,要善于把它们有机地联系起来,相互转化和相互变用.
1.解不等式的核心问题是不等式的同解变形,不等式的性质则是不等式变形的理论依据,方程的根、函数的性质和图象都与不等式的解法密切相关,要善于把它们有机地联系起来,互相转化.在解不等式中,换元法和图解法是常用的技巧之一.通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数、数形结合,则可将不等式的解化归为直观、形象的图形关系,对含有参数的不等式,运用图解法可以使得分类标准明晰.
21.已知 ,奇函数
,奇函数 在
在 上单调.
上单调.
(Ⅰ)求字母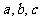 应满足的条件;
应满足的条件;
(Ⅱ)设 ,且满足
,且满足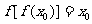 ,求证:
,求证: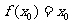 .
.
20.已知偶函数f(x)=cosqsinx-sin(x-q)+(tanq-2)sinx-sinq的最小值是0,求f(x)的最大值 及此时x的集合.
19. 设f(x)=lg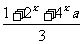 ,如果当x∈(-∞,1]时f(x)有意义,求
实数a的取值范围。
,如果当x∈(-∞,1]时f(x)有意义,求
实数a的取值范围。
18. 已知△ABC三内角A、B、C的大小成等差数列,且tanA·tanC=2+ ,又知顶点C的对边c上的高等于4
,又知顶点C的对边c上的高等于4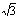 ,求△ABC的三边a、b、c及三内角。
,求△ABC的三边a、b、c及三内角。
17. 如图,AB是圆O的直径,PA垂直于圆O所在平面,C是圆周上任一点,设∠BAC=θ,PA=AB=2r,求异面直线PB和AC的距离。
16. 设等差数列{a }的前n项的和为S
}的前n项的和为S ,已知a
,已知a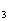 =12,S
=12,S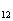 >0,S
>0,S <0 。
<0 。
①.求公差d的取值范围;
②.指出S 、S
、S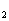 、…、S
、…、S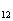 中哪一个值最大,并说明理由。(1992年全国高考)
中哪一个值最大,并说明理由。(1992年全国高考)
        P
M
A
H
B
D C P
M
A
H
B
D C |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com