2.证明三角等式的思路和方法。

(1)思路：利用三角公式进行化名，化角，改变运算结构，使等式两边化为同一形式。

(2)证明方法：综合法、分析法、比较法、代换法、相消法、数学归纳法。

1.三角函数恒等变形的基本策略。

(1)常值代换：特别是用“1”的代换，如1=cos²θ+sin²θ=tanx·cotx=tan45°等。

(2)项的分拆与角的配凑。如分拆项：sin²x+2cos²x=(sin²x+cos²x)+cos²x=1+cos²x；配凑角：α=(α+β)－β，β=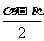－等。

(3)降次与升次。(4)化弦(切)法。

(4)引入辅助角。asinθ+bcosθ=sin(θ+)，这里辅助角所在象限由a、b的符号确定，角的值由tan=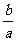确定。

2004年各地高考中本部分所占分值在17-22分，主要以选择题和解答题的形式出现。主要考察内容按综合难度分，我认为有以下几个层次：

第一层次：通过诱导公式和倍角公式的简单运用，解决有关三角函数基本性质的问题。如判断符号、求值、求周期、判断奇偶性等。

第二层次：三角函数公式变形中的某些常用技巧的运用。如辅助角公式、平方公式逆用、切弦互化等。

第三层次：充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质，解决较复杂的函数问题。如分段函数值，求复合函数值域等。

2．熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质，并能用它研究复合函数的性质；熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状、特点，并会用五点画出函数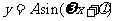的图象；理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化．

1．熟练掌握三角变换的所有公式，理解每个公式的意义，应用特点，常规使用方法等；熟悉三角变换常用的方法--化弦法，降幂法，角的变换法等；并能应用这些方法进行三角函数式的求值、化简、证明；掌握三角变换公式在三角形中应用的特点，并能结合三角形的公式解决一些实际问题．

(五)用递推方法解题

11、(03年全国)设{a_n}是首项为1的正项数列，且(n+1)a²_n+1-na_n²+a_n+1a_n=0,求它的通项公式是__1/n

12、(04年全国)已知数列{a_n}满足a.₁=1,a_n=a₁+2a₂+3a₃+---+(n-1)a_n-1 (n>1),则{a_n}的通项a_n=______a₁=1;a_n=n2　

13、(04年北京)定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和。

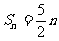已知数列是等和数列，且，公和为5，那么的值为__3___，这个数列的前n项和的计算公式为__当n为偶数时，；当n为奇数时，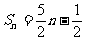

14. (04年全国)已知数列{a_n}中，a₁=1，a_2k=a_2k-1+(-1)^K,a_2k+1=a_2k+3^k,其中k=1,2,3，…。

(1)求a_3,a₅；　　 (2)求{a_n}的通项公式

解：(I)a₂=a₁+(－1)¹=0, a₃=a₂+3¹=3.a₄=a₃+(－1)²=4 　a₅=a₄+3²=13, 　所以，a₃=3,a₅=13.

　　 (II)　 a_2k+1=a_2k+3^k = a_2k－1+(－1)^k+3^k,　　 所以a_2k+1－a_2k－1=3^k+(－1)^k,

　　 同理a_2k－1－a_2k－3=3^k－1+(－1)^k－1,　　　 a₃－a₁=3+(－1).

　　 所以(a_2k+1－a_2k－1)+(a_2k－1－a_2k－3)+…+(a₃－a₁)

　　　　 =(3^k+3^k－1+…+3)+[(－1)^k+(－1)^k－1+…+(－1)],

　　 由此得a_2k+1－a₁=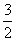(3^k－1)+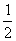[(－1)^k－1],

　　 于是a_2k+1=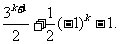a_2k= a_2k－1+(－1)^k=(－1)^k－1－1+(－1)^k=(－1)^k=1.

{a_n}的通项公式为：

　　 当n为奇数时，a_n­=

　 　当n为偶数时，

(四)用函数方法解题　　　　　　　　　　　　

8、(04年天津)已知数列{a_n},那么“对任意的nN₊,点P_n(n ,a_n)都在直线y=x+1上”是“{a_n}为等差数列”的( B)

A必要条件　 B 充分条件　 C　 充要条件　 D　 既不充分也不必要条件

9、(99年上海)已知等差数列{a_n}满足3a₄=7a₇,且a₁>0,S_n是{a_n}的前n项和，S_n取得最大值，则n=___9______.

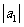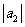10、(01年上海)已知数列{a_n}中a_n=2n-7,(nN₊),++--+=_153___　

(三)用整体化方法解题

5、(00年)已知等差数列{a_n}满足a₁+a₂+a₃+…+a₁₀₁=0,则有(C )　　　　　　　

　 A　 a₁+a₁₀₁>0　　 B　 a₂+a₁₀₀<0　　 C　 a₃+a₉₉=0　　 D　 a₅₁=51

6、(02年)若一个等差数列的前3项和为34，最后3项的和为146，且所有项的和为390，则这个数列的项数为(A)　　　　　　　　　

　　 A　 13　　　　 B　 12　　　　 C 11　　　　　　 D 10

7、(03年上海)在等差数列{a_n}中a₅=3，a₆=-2,a₄+a₅+…+a₁₀=-49

(二)用赋值法解题

2、(96年)等差数列{a_n}的前m项和为30，前2m项和为100，则它的前3m项和为(C )

A　 130　　　　 B　 170　　　 C　 210　　　 D　 260

3、(01年)设{a_n}是公比为q的等比数列， S_n是{a_n}的前n项和,若{S_n}是等差数列，则q=__1_

4、设数列{a_n}的前项的和S_n= (对于所有n1)，且a₄=54,则a₁=__2___

(一)用基本量方法解题

1、(04年浙江)已知等差数列的公差为2，若a_1,a₃,a₄成等比数列，则a₂= (B )

A　 －4　　 B －6　　　 C －8　　　　 D －10