
16.从1,2,……,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是(C )
A.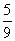 B.
B.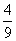 C.
C.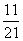 D.
D.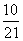
15.(本小题满分12分)
一接待中心有A、B、C、D四部热线电话,已知某一时刻电话A、B占线的概率均为0.5,电话C、D占线的概率均为0.4,各部电话是否占线相互之间没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概率分布和它的期望.
解:本小题主要考查离散型随机变量分布列和数学期望等概念.考查运用概率知识解决实际问题的能力.满分12分.
解:P(ξ=0)=0.52×0.62=0.09.
P(ξ=1)=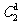 ×0.52×0.62+
×0.52×0.62+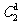 ×0.52×0.4×0.6=0.3
×0.52×0.4×0.6=0.3
P(ξ=2)= 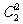 ×0.52×0.62+
×0.52×0.62+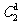
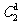 ×0.52×0.4×0.6+
×0.52×0.4×0.6+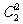 ×0.52×0.42=0.37.
×0.52×0.42=0.37.
P(ξ=3)= 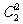
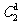 ×0.52×0.4×0.6+
×0.52×0.4×0.6+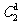
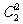 ×0.52×0.42=0.2
×0.52×0.42=0.2
P(ξ=4)= 0.52×0.42=0.04
于是得到随机变量ξ的概率分布列为:
|
ξ |
0 |
1 |
2 |
3 |
4 |
|
P |
0.09 |
0.3 |
0.37 |
0.2 |
0.04 |
所以Eξ=0×0.09+1×0.3+2×0.37+3×0.2+4×0.04=1.8.
14.从数字1,2,3,4,5,中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为 ( D )
A.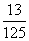 B.
B.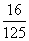 C.
C.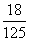 D.
D.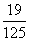
13. 设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
(Ⅰ)三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标概率;(Ⅱ)若甲单独向目标射击三次,求他恰好命中两次的概率. (2004年重庆卷)
12.为防止某突发事件发生,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率(记为P)和所需费用如下:
|
预防措施 |
甲 |
乙 |
丙 |
丁 |
|
P |
0.9 |
0.8 |
0.7 |
0.6 |
|
费用(万元) |
90 |
60 |
30 |
10 |
预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前
提下,请确定一个预防方案,使得此突发事件不发生的概率最大.(2004年湖北卷)
解:方案1:单独采用一种预防措施的费用均不超过120万元.由表可知,采用甲措施,可使此突发事件不发生的概率最大,其概率为0.9.
方案2:联合采用两种预防措施,费用不超过120万元,由表可知.联合甲、丙两种预防措施可使此突发事件不发生的概率最大,其概率为1-(1-0.9)(1-0.7)=0.97.
方法3:联合采用三种预防措施,费用不超过120万元,故只能联合乙、丙、丁三种预防措施,此时突发事件不发生的概率为1-(1-0.8)(1-0.7)(1-0.6)=1-0.024=0.976.
综合上述三种预防方案可知,在总费用不超过120万元的前提下,联合使用乙、丙、丁三种预防措施可使此突发事件不发生的概率最大.
11. 甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为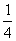 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为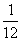 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为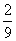 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
(2004年湖南卷)
10. 甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)分别求甲、乙两人考试合格的概率;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率. (2004年福建卷)
9. 某地区有5个工厂,由于用电紧缺,规定每个工厂在一周内必须选择某一天停电
(选哪一天是等可能的).假定工厂之间的选择互不影响.
(Ⅰ)求5个工厂均选择星期日停电的概率;
(Ⅱ)求至少有两个工厂选择同一天停电的概率. (2004年浙江卷)
8. 从4名男生和2名女生中任选3人参加演讲比赛.
(Ⅰ)求所选3人都是男生的概率;
(Ⅱ)求所选3人中恰有1名女生的概率;
(Ⅲ)求所选3人中至少有1名女生的概率. (2004年天津卷)
7.某同学参加科普知识竞赛,需回答3个问题.竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(Ⅰ)求这名同学得300分的概率;
(Ⅱ)求这名同学至少得300分的概率. (2004年全国卷Ⅲ)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com