
6. 冰箱中放有甲、乙两种饮料各5瓶,每次饮用时从中任意取1瓶甲种或乙种饮料,取用甲种或乙种饮料的概率相等.
(Ⅰ)求甲种饮料饮用完毕而乙种饮料还剩下3瓶的概率;
(Ⅱ)求甲种饮料被饮用瓶数比乙种饮料被饮用瓶数至少多4瓶的概率.
例题答案
1(Ⅰ)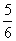 ;(Ⅱ)
;(Ⅱ)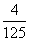 2(Ⅰ)
2(Ⅰ)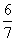 ;(Ⅱ)
;(Ⅱ)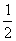 . 3(Ⅰ)0.228;(Ⅱ)0.564. 4(Ⅰ)
. 3(Ⅰ)0.228;(Ⅱ)0.564. 4(Ⅰ)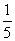 ;(Ⅱ)
;(Ⅱ)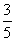 ;(Ⅲ)
;(Ⅲ)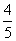 .
.
作业答案
5. 已知10件产品中有3件是次品.
(I)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(II)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
4. 某国际科研合作项目成员由11个美国人、4个法国人和5个中国人组成。现从中随机
选出两位作为成果发布人,则此两人不属于同一个国家的概率为
(结果用分数表示)
3. 在某次花样滑冰比赛中,发生裁判受贿事件,竞赛委员会决定将裁判曰原来的9名增至14名,但只任取其中7名裁判的评分作为有效分,若14名裁判中有2人受贿,则有效分中没有受贿裁判的评分的概率是 .(结果用数值表示)
2. 在5张卡片上分别写着数字1、2、3、4、5,然后把它们混合,再任意排成一行,则得到的数能被5或2整除的概率是( )
(A) 0.8 (B) 0.6 (C) 0.4 (D) 0.2
1. 将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩
具)先后抛掷3次,至少出现一次6点向上的概率是 ( )
(A) (B) (C) (D)
6.解: 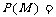
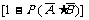
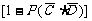 =0.752
=0.752
第三课时
例题
例1 从10位同学(其中6女,4男)中随机选出3位参加测验.每位女同学能通过测验的概率均为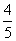 ,每位男同学能通过测验的概率均为
,每位男同学能通过测验的概率均为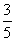 .试求:
.试求:
(Ⅰ)选出的3位同学中,至少有一位男同学的概率;
(Ⅱ)10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.
(2004年全国卷Ⅰ)
例2 已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.求:
(Ⅰ)A、B两组中有一组恰有两支弱队的概率;
(Ⅱ)A组中至少有两支弱队的概率. (2004年全国卷Ⅱ)
例3 某同学参加科普知识竞赛,需回答3个问题.竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(Ⅰ)求这名同学得300分的概率;
(Ⅱ)求这名同学至少得300分的概率. (2004年全国卷Ⅲ)
例4 从4名男生和2名女生中任选3人参加演讲比赛.
(Ⅰ)求所选3人都是男生的概率;
(Ⅱ)求所选3人中恰有1名女生的概率;
(Ⅲ)求所选3人中至少有1名女生的概率. (2004年天津卷)
备用 A、B、C、D、E五人分四本不同的书,每人至多分一本,求:
(1)A不分甲书,B不分乙书的概率;
(2)甲书不分给A、B,乙书不分给C的概率。
解: (1)分别记“分不到书的是A,B不分乙书”,“分不到书的是B,A不分甲书”,“分不到书的是除A,B以外的其余的三人中的一人,同时A不分甲书,B不分乙书”为事件A1,B1,C1,它们的概率是
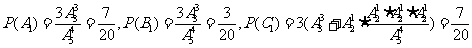 .
.
因为事件A1,B1,C1彼此互斥,由互斥事件的概率加法公式,A不分甲书,B不分乙书的概率是: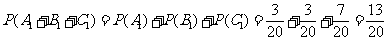
(2) 在乙书不分给C的情况下,分别记“甲书分给C”,“甲书分给D”,“甲书分给E”为事件A2,B2,C2彼此互斥,有互斥事件的概率加法公式,甲书不分给A,B,乙书不分给C的概率为: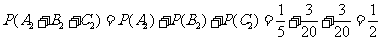
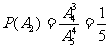
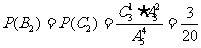
作业
1. D 2. A 3.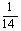 4.
4. 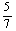 5.解:有两种可能:将原1件次品仍鉴定为次品,原3件正品中1件错误地鉴定为次品;将原1件次品错误地鉴定为正品,原3件正品中的2件错误地鉴定为次品. 概率为
5.解:有两种可能:将原1件次品仍鉴定为次品,原3件正品中1件错误地鉴定为次品;将原1件次品错误地鉴定为正品,原3件正品中的2件错误地鉴定为次品. 概率为
P=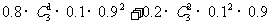 =0.1998
=0.1998
1. (Ⅰ) 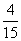 ; (Ⅱ)
; (Ⅱ)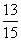 .
2. 0.648; 0.792. 3. (Ⅰ)
.
2. 0.648; 0.792. 3. (Ⅰ) 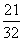 ; (Ⅱ) 5人. 4. (Ⅰ) 0.176 ; (Ⅱ) 0.012 .
; (Ⅱ) 5人. 4. (Ⅰ) 0.176 ; (Ⅱ) 0.012 .
作业答案
6.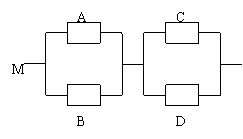 如图,用
如图,用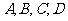 表示四类不同的元件连接成系统
表示四类不同的元件连接成系统 .当元件
.当元件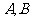 至少有一个正常工作且元件
至少有一个正常工作且元件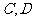 至少有一个正常工作时,系统
至少有一个正常工作时,系统
正常工作.已知元件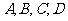 正常工作的概率
正常工作的概率
依次为0.5,0.6,0.7,0.8,求元件连接成的系
统 正常工作的概率
正常工作的概率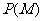 .
.
例题答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com