3．要能正确求导，必须做到以下两点：

(1)熟练掌握各基本初等函数的求导公式以及和、差、积、商的求导法则，复合函数的求导法则。

(2)对于一个复合函数，一定要理清中间的复合关系，弄清各分解函数中应对哪个变量求导。

2．利用导数判别可导函数的极值的方法及求一些实际问题的最大值与最小值．

复合函数的求导法则是微积分中的重点与难点内容。课本中先通过实例，引出复合函数的求导法则，接下来对法则进行了证明。

1．导数概念的理解．

3．导数与解析几何或函数图象的混合问题是一种重要类型，也是高考中考察综合能力的一个方向，应引起注意。

2．关于函数特征，最值问题较多，所以有必要专项讨论，导数法求最值要比初等方法快捷简便。

导数是微积分的初步知识，是研究函数，解决实际问题的有力工具。在高中阶段对于导数的学习，主要是以下几个方面:

1．导数的常规问题：

(1)刻画函数(比初等方法精确细微)；(2)同几何中切线联系(导数方法可用于研究平面曲线的切线)；(3)应用问题(初等方法往往技巧性要求较高，而导数方法显得简便)等关于次多项式的导数问题属于较难类型。

1． 假设每一架飞机引擎飞机中故障率为P，且个引擎是否发生故障是独立的，如果有至少50%的引擎能正常运行，问对于多大的P而言，4引擎飞机比2引擎飞机更安全？

解　 飞机成功飞行的概率：

^{4引擎飞机为：}

2引擎飞机为：

要使4引擎飞机比2引擎飞机更安全，只要

所以

1． 在100件产品中，有95件合格品，5件次品，从中任取2件，求：

(1)　 2件都是合格品的概率；

(2)　 2件都是次品的概率；

(3)1件是合格品，1件是次品的概率。

解　 从100件产品中任取2件的可能出现的结果数，就是从100个元素中任取2个元素的组合数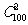，由于任意抽取，这些结果出现的可能性相等.为基本事件总数.

(1)00件产品中有95件合格品，取到2件合格品的结果数，就是从95个元素中任取2个组合数，记“任取2件都是合格品”为事件A₁，那么

(2)由于在100件产品中有5件次品，取到2件次品的结果数为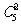.记“任取2件都是次品”为事件A₂,那么事件A₂的概率为：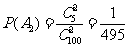

(3)记“任取2件，1件是次品，1件是合格品”为种，则事件A₃的概率为：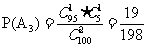

备用课时三　 相互独立事件同时发生的概率

例题

例1 猎人在距离100米处射击一野兔，其命中率为0.5，如果第一次射击未中，则猎人进行第二次射击，但距离150米. 如果第二次射击又未中，则猎人进行第三次射击，并且在发射瞬间距离为200米. 已知猎人的命中概率与距离的平方成反比，求猎人命中野兔的概率.

解　 记三次射击依次为事件A，B，C，其中,由，求得k=5000。

,命中野兔的概率为

例2　 1个产品要经过2道加工程序，第一道工序的次品率为3%，第二道工序次品率为2%，求产品的次品率.

解　 设“第一道工序出现次品“为事件A，“第二道工序出现次品”为事件B，“至少有一道工序出现次品”该产品就是次品，所求概率为

例3　 如图，某电子器件是由三个电阻组成的回路，其中共有六个焊接点A、B、C、D、E、F，如果某个焊接点脱落，整个电路就会不通。每个焊接点脱落的概率均是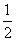，现在发现电路不通了，那么至少有两个焊接点脱落的概率是多少？

解：

例4　 要制造一种机器零件，甲机床废品率为0.05，而乙机床废品率为0.1，而它们的生产是独立的，从它们制造的产品中，分别任意抽取一件，求：

(1)其中至少有一件废品的概率； (2)其中至多有一件废品的概率.

解： 设事件A为“从甲机床抽得的一件是废品”；B为“从乙机床抽得的一件是废品”.

则P(A)=0.05,　 P(B)=0.1,

(1)至少有一件废品的概率

(2)至多有一件废品的概率

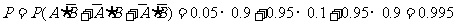
作业

1． 袋中有a只黑球b只白球，它们除颜色不同外，没有其它差别，现在把球随机地一只一只摸出来，求第k次摸出的球是黑球的概率.

解法一：把a只黑球和b只白球都看作是不同的，将所有的球都一一摸出来放在一直线上的a+b个位置上，把所有的不同的排法作为基本事件的全体，则全体基本事件的总数为(a+b)！，而有利事件数为a(a+b-1)!故所求概率为P=。

解法二：把a只黑球和b只白球看作是不同的，将前k次摸球的所有不同可能作为基本事件全体，总数为，有利事件为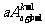，故所求概率为P=

解法三：把只考虑k次摸出球的每一种可能作为基本事件，总数为a+b，有利事件为a,故所求概率为.

备用课时二　 互斥事件有一个发生的概率

例题

例1 房间里有6个人，求至少有2个人的生日在同一月内的概率.

解　 6个人生日都不在同一月内的概率P()=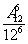.故所求概率为P(A)=1-P()=1-.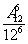

例2 从一副52张的扑克牌中任取4张，求其中至少有两张牌的花色相同的概率。

解法1 任取四张牌，设至少有两张牌的花色相同为事件A；四张牌是同一花色为事件B₁；有3张牌是同一花色，另一张牌是其他花色为事件B₂；每两张牌是同一花色为事件B₃；只有两张牌是同一花色，另两张牌分别是不同花色为事件B₄，可见，B₁,B₂,B₃,B₄彼此互斥，且A=B₁+B₂+B₃+B₄。

P(B₁)= , P(B₂)= ,

　 P(B₃)= , P(B₄)= ,

　 P(A)=P(B₁)+P(B₂)+P(B₃)+P(B₄) 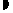0.8945

解法2 设任取四长牌中至少有两张牌的花色相同为事件A，则为取出的四张牌的花色各不相同，　　 P()=，

答：至少有两张牌花色相同的概率是0.8945

例3 在20件产品中有15件正品，5件次品，从中任取3件，求：

(1)恰有1件次品的概率；(2)至少有1件次品的概率.

解 (1)从20件产品中任取3件的取法有，其中恰有1件次品的取法为。

恰有一件次品的概率P=.

(2)法一 从20件产品中任取3件，其中恰有1件次品为事件A₁,恰有2件次品为事件A₂，3件全是次品为事件A₃,则它们的概率

P(A₁)= =,,,

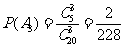而事件A₁、A₂、A₃彼此互斥，因此3件中至少有1件次品的概率

P(A₁+A₂+A₃)=P(A₁)+P(A₂)+P(A₃)= .

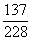法二 记从20件产品中任取3件，3件全是正品为事件A，那么任取3件，至少有1件次品为，根据对立事件的概率加法公式P()=

例4　 1副扑克牌有红桃、黑桃、梅花、方块4种花色，每种13张，共52张，从1副洗好的牌中任取4张，求4张中至少有3张黑桃的概率.

解　 从52张牌中任取4张，有种取法.“4张中至少有3张黑桃”，可分为“恰有3张黑桃”和“4张全是黑桃”，共有种取法

注　 研究至少情况时，分类要清楚。

作业

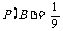6.(Ⅰ)①,②; (Ⅱ),,故A与B是不独立的．

备用课时一　 随机事件的概率

例题

例1　 某人有5把钥匙，但忘记了开房门的是哪一把，于是，他逐把不重复地试开，问：

(1)恰好第三次打开房门所的概率是多少？

(2)三次内打开的概率是多少？

(3)如果5把内有2把房门钥匙，那么三次内打开的概率是多少？

解　 5把钥匙，逐把试开有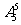种结果，由于该人忘记了开房间的是哪一把，因此这些结果是等可能的。

(1)第三次打开房门的结果有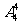种，故第三次打开房门锁的概率P(A)==

(2)三次内打开房门的结果有种，因此所求概率P(A)= =

(3)方法1　 因5把内有2把房门钥匙，故三次内打不开的结果有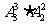种，从而三次内打开的结果有种，从而三次内打开的结果有种，所求概率P(A)= =.

方法2　 三次内打开的结果包括：三次内恰有一次打开的结果种；三次内恰有两次打开的结果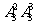种.因此，三次内打开的结果有()种，所求概率P(A)=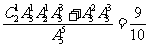

例2 　某商业银行为储户提供的密码有0，1，2，…，9中的6个数字组成.

(1)某人随意按下6个数字，按对自己的储蓄卡的密码的概率是多少？

(2)某人忘记了自己储蓄卡的第6位数字，随意按下一个数字进行试验，按对自己的密码的概率是多少？

解 (1)储蓄卡上的数字是可以重复的，每一个6位密码上的每一个数字都有0，1，2，…，9这10种，正确的结果有1种，其概率为，随意按下6个数字相当于随意按下个，随意按下6个数字相当于随意按下个密码之一，其概率是.

(2)以该人记忆自己的储蓄卡上的密码在前5个正确的前提下，随意按下一个数字，等可能性的结果为0，1，2，…，9这10种，正确的结果有1种，其概率为.

例3 　一个口袋内有m个白球和n个黑球，从中任取3个球，这3个球恰好是2白1黑的概率是多少？(用组合数表示)

解　 设事件I是“从m个白球和n个黑球中任选3个球”，要对应集合I₁，事件A是“从m个白球中任选2个球，从n个黑球中任选一个球”，本题是等可能性事件问题，且Card(I₁)= ，于是P(A)=.

例4　 将一枚骰子先后抛掷2次，计算:

(1)一共有多少种不同的结果.

(2)其中向上的数之积是12的结果有多少种？

(3)向上数之积是12的概率是多少？

解 (1)将骰子向桌面先后抛掷两次，一共有36种不同的结果.

(2)向上的数之积是12，记(I,j)为“第一次掷出结果为I，第二次掷出结果为j”则相乘为12的结果有(2，6)，(3，4)，(4，3)，(6，2)4种情况.

(3)由于骰子是均匀的，将它向桌面先后抛掷2次的所有36种结果是等可能的，其中“向上的数之积是12”这一事件记为A.Card(A)=4.所以所求概率P(A)= =.

作业