
1、提问:正方形面积公式?正方体的体积公式?(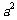 、
、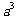 )
)
由于向量具有几何形式和代数形式的“双重身份”,使向量与解析几何之间有着密切联系,而新课程高考则突出了对向量与解析几何结合考查,这就要求我们在平时的解析几何教学与复习中,应抓住时机,有效地渗透向量有关知识,树立应用向量的意识。应充分挖掘课本素材,在教学中从推导有关公式、定理,例题讲解入手,让学生去品位、去领悟,在公式、定理的探索、形成中逐渐体会向量的工具性,逐渐形成应用向量的意识,在教学中还应注重引导学生善于运用一些问题的结论,加以引申,使之成为解题方法,体会向量解题的优越性,在教学中还应注重引导学生善于运用向量方法解题,逐步树立运用向量知识解题的意识。
例1、(2000年全国高考题)椭圆 的焦点为F
的焦点为F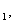 F
F ,点P为其上的动点,当∠F
,点P为其上的动点,当∠F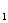 P F
P F 为钝角时,点P横坐标的取值范围是___。
为钝角时,点P横坐标的取值范围是___。
解:F1(-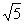 ,0)F2(
,0)F2(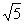 ,0),设P(3cos
,0),设P(3cos ,2sin
,2sin )
)
 为钝角
为钝角
∴ 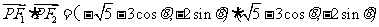
=9cos2 -5+4sin2
-5+4sin2 =5 cos2
=5 cos2 -1<0
-1<0
解得: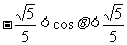 ∴点P横坐标的取值范围是(
∴点P横坐标的取值范围是( )
)
点评:解决与角有关的一类问题,总可以从数量积入手。本题中把条件中的角为钝角转化为向量的数量积为负值,通过坐标运算列出不等式,简洁明了。
例2、已知定点A(-1,0)和B(1,0),P是圆(x-3)2+(y-4)2=4上的一动点,求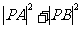 的最大值和最小值。
的最大值和最小值。
分析:因为O为AB的中点,所以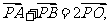 故可利用向量把问题转化为求向量
故可利用向量把问题转化为求向量 的最值。
的最值。
解:设已知圆的圆心为C,由已知可得: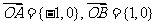
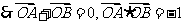 又由中点公式得
又由中点公式得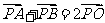
 所以
所以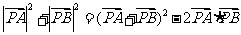
=
=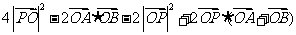
=
又因为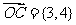 点P在圆(x-3)2+(y-4)2=4上,
点P在圆(x-3)2+(y-4)2=4上,
所以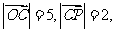 且
且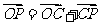
所以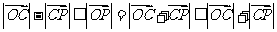
即
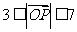 故
故
所以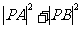 的最大值为100,最小值为20。
的最大值为100,最小值为20。
点评:有些解几问题虽然没有直接用向量作为已知条件出现,但如果运用向量知识来解决,也会显得自然、简便,而且易入手。
例3、(2003年天津高考题)O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足 ,
, ,则P的轨迹一定通过△ABC的( )
,则P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
分析:因为 同向的单位向量,由向量加法的平行四边形则知
同向的单位向量,由向量加法的平行四边形则知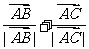 是与∠ABC的角平分线(射线)同向的一个向量,又
是与∠ABC的角平分线(射线)同向的一个向量,又 ,知P点的轨迹是∠ABC的角平分线,从而点P的轨迹一定通过△ABC的内心。
,知P点的轨迹是∠ABC的角平分线,从而点P的轨迹一定通过△ABC的内心。
反思:根据本题的结论,我们不难得到求一个角的平分线所在的直线方程的步骤;
(1)
由顶点坐标(含线段端点)或直线方程求得角两边的方向向量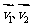 ;
;
(2)
求出角平分线的方向向量
(3)
由点斜式或点向式得出角平分线方程。{直线的点向式方程:过P(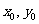 ),其方向向量为
),其方向向量为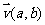 ,其方程为
,其方程为 }
}
例4、(2003年天津)已知常数 ,向量
,向量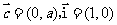 ,经过原点
,经过原点 以
以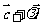 为方向向量的直线与经过定点
为方向向量的直线与经过定点 以
以 为方向向量的直线相交于点
为方向向量的直线相交于点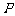 ,其中
,其中 .试问:是否存在两个定点
.试问:是否存在两个定点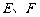 ,使得
,使得 为定值,若存在,求出
为定值,若存在,求出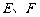 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力.)
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵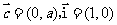 , ∴
, ∴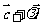 =(λ,a),
=(λ,a), =(1,-2λa).
=(1,-2λa).
因此,直线OP和AP的方程分别为 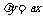 和
和 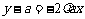 .
.
消去参数λ,得点 的坐标满足方程
的坐标满足方程 .
.
整理得  ……① 因为
……① 因为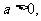 所以得:
所以得:
(i)当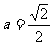 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ii)当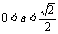 时,方程①表示椭圆,焦点
时,方程①表示椭圆,焦点 和
和 为合乎题意的两个定点;
为合乎题意的两个定点;
(iii)当 时,方程①也表示椭圆,焦点
时,方程①也表示椭圆,焦点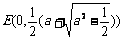 和
和 为合乎题意的两个定点.
为合乎题意的两个定点.
点评:本题以平面向量为载体,考查求轨迹的方法、利用方程判定曲线的性质、曲线与方程的关系等解析几何的基本思想和综合解题能力。去掉平面向量的背景,我们不难看到,本题即为下题:
在△OAP中,O(0,0)、A(0,a)为两个定点,另两边OP与AP的斜率分别是 ,求P的轨迹。
,求P的轨迹。
而课本上有一道习题(数学第二册(上)第96页练习题4):
三角形ABC的两个顶点A、B的坐标分别是(-6,0)、(6,0),边AC、BC所在直线的斜率之积等于 ,求顶点C的轨迹方程。通过本例可见高考题目与课本的密切关系。
,求顶点C的轨迹方程。通过本例可见高考题目与课本的密切关系。
例5.(2004年天津卷理22)椭圆的中心是原点O,它的短轴长为 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(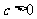 )的准线
)的准线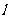 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(1)求椭圆的方程及离心率;
(2)若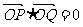 ,求直线PQ的方程;
,求直线PQ的方程;
(3)设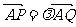 (
( ),过点P且平行于准线
),过点P且平行于准线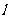 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明 .
.
分析:本小题主要考查椭圆的标准方程和几何性质,直线方程,平面向量的计算,曲线和方程的关系等解析几何的基本思想方法和综合解题能力.
(1)解:由题意,可设椭圆的方程为 .
.
由已知得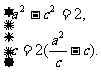 解得
解得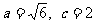
所以椭圆的方程为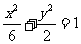 ,离心率
,离心率 .
.
(2)解:由(1)可得A(3,0).
设直线PQ的方程为 .由方程组
.由方程组
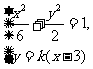 得
得
依题意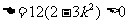 ,得
,得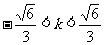 .
.
设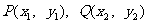 ,则
,则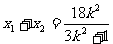 , ①
, ①  . ②
. ②
由直线PQ的方程得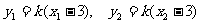 .于是
.于是
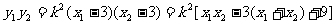 . ③
. ③
∵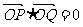 ,∴
,∴ . ④
. ④
由①②③④得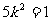 ,从而
,从而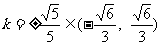 .
.
所以直线PQ的方程为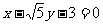 或
或
(2)证明: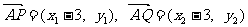 .由已知得方程组
.由已知得方程组
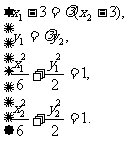 注意
注意 ,解得
,解得
因 ,故
,故

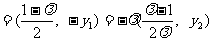 .
.
而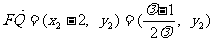 ,所以
,所以 .
.
平面向量是高中数学的新增内容,也是新高考的一个亮点。 向量知识、向量观点在数学、物理等学科的很多分支有着广泛的应用,它具有代数形式和几何形式的“双重身份”,能融数形与一体,能与中学数学教学内容的的许多主干知识综合,形成知识交汇点。而在高中数学体系中,解析几何占有着很重要的地位,有些问题用常规方法去解决往往运算比较繁杂,不妨运用向量作形与数的转化,则会大大简化过程。
4.(天津卷20)(本小题满分12分) 已知函数 在
在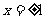 处取得极值。
处取得极值。
(I)讨论 和
和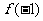 是函数
是函数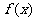 的极大值还是极小值;
的极大值还是极小值;
(II)过点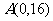 作曲线
作曲线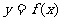 的切线,求此切线方程。
的切线,求此切线方程。
(江苏卷10)函数 在闭区间[-3,0]上的最大值、最小值分别是 ( )
在闭区间[-3,0]上的最大值、最小值分别是 ( )
(A)1,-1 (B)1,-17 (C)3,-17 (D)9,-19
 (浙江卷11)设f '(x)是函数f(x)的导函数,y=f '(x)的图象
(浙江卷11)设f '(x)是函数f(x)的导函数,y=f '(x)的图象
如右图所示,则y=f(x)的图象最有可能的是

(A) (B) (C) (D)
(浙江卷20)设曲线y=e-x(x≥0)在点M(t,e-t}处的切线l与x轴、y轴围成的三角形面积为S(t). (1)求切线l的方程;(2)求S(t)的最大值。
3.(天津卷9)函数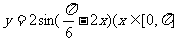 )为增函数的区间是
)为增函数的区间是
(A)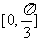 (B)
(B)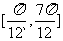 (C)
(C)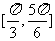 (D)
(D)
2.(全国卷22)(本小题满分14分)已知函数f(x)=ln(1+x)-x,g(x)=xlnx,
(i)求函数f(x)的最大值;(ii)设0<a<b,证明0<g(a)+g(b)-2g( )<(b-a)ln2.
)<(b-a)ln2.
1.(全国卷10)函数y=xcosx-sinx在下面哪个区间内是增函数( )
A ( ) B (π,2π) C (
) B (π,2π) C (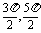 ) D (2π,3π)
) D (2π,3π)
例1.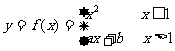 在
在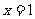 处可导,则
处可导,则
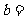
思路: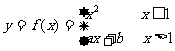 在
在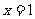 处可导,必连续
处可导,必连续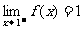
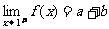
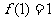 ∴
∴
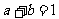

 ∴
∴ 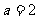
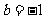
例2.已知f(x)在x=a处可导,且f′(a)=b,求下列极限:
(1)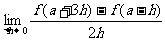 ; (2)
; (2)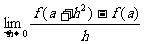
分析:在导数定义中,增量△x的形式是多种多样,但不论△x选择哪种形式,△y也必须选择相对应的形式。利用函数f(x)在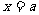 处可导的条件,可以将已给定的极限式恒等变形转化为导数定义的结构形式。
处可导的条件,可以将已给定的极限式恒等变形转化为导数定义的结构形式。
解:(1)
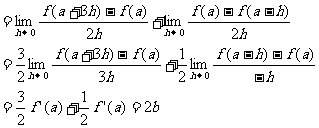
(2)
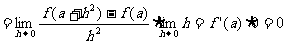
说明:只有深刻理解概念的本质,才能灵活应用概念解题。解决这类问题的关键是等价变形,使极限式转化为导数定义的结构形式。
例3.观察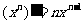 ,
, ,
, ,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
解:若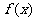 为偶函数
为偶函数 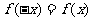 令
令
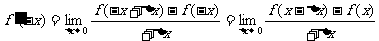

∴ 可导的偶函数的导函数是奇函数
另证:
∴ 可导的偶函数的导函数是奇函数
例4.(1)求曲线 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;
(2)运动曲线方程为 ,求t=3时的速度。
,求t=3时的速度。
分析:根据导数的几何意义及导数的物理意义可知,函数y=f(x)在 处的导数就是曲线y=f(x)在点
处的导数就是曲线y=f(x)在点 处的切线的斜率。瞬时速度是位移函数S(t)对时间的导数。
处的切线的斜率。瞬时速度是位移函数S(t)对时间的导数。
解:(1) ,
,
 ,即曲线在点(1,1)处的切线斜率k=0
,即曲线在点(1,1)处的切线斜率k=0
因此曲线 在(1,1)处的切线方程为y=1
在(1,1)处的切线方程为y=1
(2)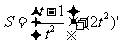
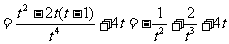
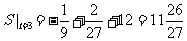 。
。
例5. 求下列函数单调区间
(1)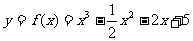 (2)
(2)
(3)
 (4)
(4)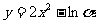
解:(1)


 时
时
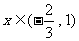
 ∴
∴ 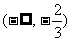 ,
,


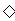
(2) ∴
∴  ,
,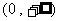

(3)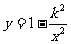
∴ 
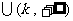

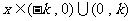

∴  ,
,
 ,
,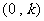
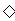
(4)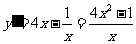 定义域为
定义域为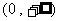
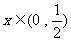




例6.求证下列不等式
(1)

(2)

(3)

证:(1)
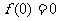

∴ 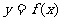 为
为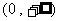 上
上 ∴
∴

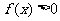 恒成立
恒成立
∴ 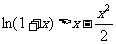
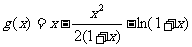
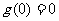
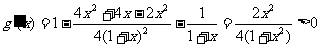
∴  在
在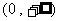 上
上 ∴
∴ 
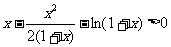 恒成立
恒成立
(2)原式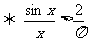 令
令 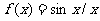

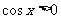

∴  ∴
∴

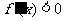

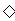
 ∴
∴ 
(3)令
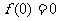
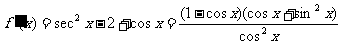

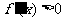 ∴
∴ 
∴ 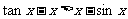
例7.利用导数求和:
(1)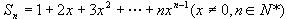 ;
;
(2)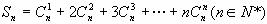 。
。
分析:这两个问题可分别通过错位相减法及利用二项式定理来解决。转换思维角度,由求导公式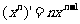 ,可联想到它们是另外一个和式的导数,利用导数运算可使问题的解决更加简捷。
,可联想到它们是另外一个和式的导数,利用导数运算可使问题的解决更加简捷。
解:(1)当x=1时,
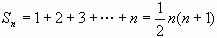 ;
;
当x≠1时,
∵ ,
,
两边都是关于x的函数,求导得
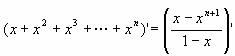
即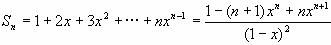
(2)∵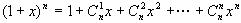 ,
,
两边都是关于x的函数,求导得 。
。
令x=1得
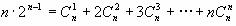 ,
,
即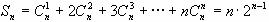 。
。
例8.设 ,求函数
,求函数 的单调区间.
的单调区间.
分析:本小题主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力.
解: .
.
当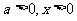 时
时 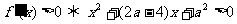 .
.

(i)当 时,对所有
时,对所有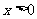 ,有
,有 .
.
即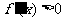 ,此时
,此时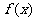 在
在 内单调递增.
内单调递增.
(ii)当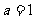 时,对
时,对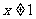 ,有
,有 ,
,
即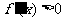 ,此时
,此时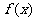 在(0,1)内单调递增,又知函数
在(0,1)内单调递增,又知函数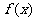 在x=1处连续,因此,
在x=1处连续,因此,
函数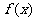 在(0,+
在(0,+ )内单调递增
)内单调递增
(iii)当 时,令
时,令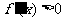 ,即
,即 .
.
解得 .
.
因此,函数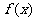 在区间
在区间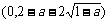 内单调递增,在区间
内单调递增,在区间
内也单调递增.
令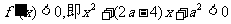 ,解得
,解得 .
.
因此,函数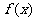 在区间
在区间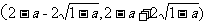 内单调递减.
内单调递减.
例9.已知抛物线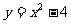 与直线y=x+2相交于A、B两点,过A、B两点的切线分别为
与直线y=x+2相交于A、B两点,过A、B两点的切线分别为 和
和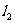 。
。
(1)求A、B两点的坐标; (2)求直线 与
与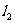 的夹角。
的夹角。
分析:理解导数的几何意义是解决本例的关键。
解 (1)由方程组
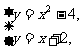 解得
A(-2,0),B(3,5)
解得
A(-2,0),B(3,5)
(2)由y′=2x,则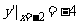 ,
, 。设两直线的夹角为θ,根据两直线的夹角公式,
。设两直线的夹角为θ,根据两直线的夹角公式,
 所以
所以
说明:本例中直线与抛物线的交点处的切线,就是该点处抛物线的切线。注意两条直线的夹角公式有绝对值符号。
例10.(2001年天津卷)设 ,
,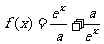 是
是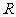 上的偶函数。
上的偶函数。
(I)求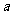 的值; (II)证明
的值; (II)证明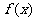 在
在 上是增函数。
上是增函数。
解:(I)依题意,对一切 有
有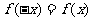 ,即
,即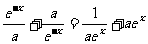 ,
,
∴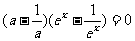 对一切
对一切 成立,
成立,
由此得到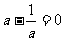 ,
,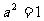 , 又∵
, 又∵ ,∴
,∴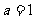 。
。
(II)证明:由 ,得
,得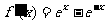
 ,
,
当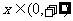 时,有
时,有 ,此时
,此时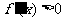 。∴
。∴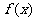 在
在 上是增函数。
上是增函数。
4.求复合函数的导数,一般按以下三个步骤进行:
(1)适当选定中间变量,正确分解复合关系;(2)分步求导(弄清每一步求导是哪个变量对哪个变量求导);(3)把中间变量代回原自变量(一般是x)的函数。
也就是说,首先,选定中间变量,分解复合关系,说明函数关系y=f(μ),μ=f(x);然后将已知函数对中间变量求导 ,中间变量对自变量求导
,中间变量对自变量求导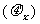 ;最后求
;最后求 ,并将中间变量代回为自变量的函数。整个过程可简记为分解--求导--回代。熟练以后,可以省略中间过程。若遇多重复合,可以相应地多次用中间变量。
,并将中间变量代回为自变量的函数。整个过程可简记为分解--求导--回代。熟练以后,可以省略中间过程。若遇多重复合,可以相应地多次用中间变量。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com