
5.对于0≤m≤4的m,不等式x2+mx>4x+m-3恒成立,则x的取值范围是____________.
4.如果一辆汽车每天行驶的路程比原来多19千米,那么在8天之内它的行程就超过2200千米;如果它每天行程比原来少12千米,那么它行驶同样的路程就得花9天多的时间,这辆汽车原来每天行程的千米数x满足:( )
A.259<x<260 B.258<x<260 C.257<x<260 D.256<x<260
[填空题]
3.已知命题p:函数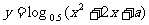 的值域为R;命题q:函数
的值域为R;命题q:函数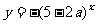 是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
A.a≤1 B.a<2 C.1<a<2 D.a≤1或a≥2
2.(2004福建)定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则 ( )
A.f(sin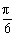 )<f(cos
)<f(cos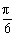 ) B.f(sin1)>f(cos1)
) B.f(sin1)>f(cos1)
C.f(cos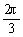 )<f(sin
)<f(sin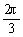 ) D.f(cos2)>f(sin2)
) D.f(cos2)>f(sin2)
1.设M=a+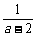 (2<a<3),N=log
(2<a<3),N=log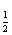 (x2+
(x2+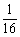 )(x∈R),那么M、N的大小关系是
)(x∈R),那么M、N的大小关系是
A.M>N B.M=N C.M<N D.不能确定
3.含有参数的不等式问题,要分析实质,灵活进行等价转化;化为熟悉的问题去解决,注意参数的范围和它对问题的影响.
2.不等式与数列的综合题,一般来说多是证明题,要熟悉不等式的常用证明方法,特别是比较法、综合法、分析法、数学归纳法等,也可利用函数的思想.
1.不等式与函数的综合是一类最常见的题目,如求函数的定义域、值域,求参数的取值范围,与函数有关的不等式证明等,解决此类综合题,要充分运用函数的单调性,注意函数的定义域,有时要与函数的奇偶性、周期性一起讨论.
[例1]已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m、n∈[-1,1],m+n≠0时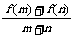 >0.
>0.
(1)用定义证明f(x)在[-1,1]上是增函数;
(2)解不等式 f(x+
f(x+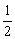 )<f(
)<f(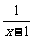 );
);
(3)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围
(1).证明 任取x1<x2,且x1,x2∈[-1,1],
任取x1<x2,且x1,x2∈[-1,1],
则f(x1)-f(x2)=f(x1)+f(-x2)
=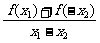 ·(x1-x2)
·(x1-x2)
∵-1≤x1<x2≤1,
∴x1+(-x2)≠0,由已知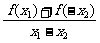 >0,又
x1-x2<0,
>0,又
x1-x2<0,
∴f(x1)-f(x2)<0,即f(x)在[-1,1]上为增函数.
(2)解 ∵f(x)在[-1,1]上为增函数,
∵f(x)在[-1,1]上为增函数,
∴ 解得:{x|-
解得:{x|-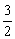 ≤x<-1,x∈R}
≤x<-1,x∈R}
(3)解 由(1)可知f(x)在[-1,1]上为增函数,且f(1)=1,
由(1)可知f(x)在[-1,1]上为增函数,且f(1)=1,
故对x∈[-1,1],恒有f(x)≤1,
所以要使f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,即要t2-2at+1≥1成立,
故t2-2at≥0,记g(a)=t2-2at,对a∈[-1,1],有
g(a)≥0,
只需g(a)在[-1,1]上的最小值大于等于0,
g(-1)≥0,g(1)≥0,
解得,t≤-2或t=0或t≥2
∴t的取值范围是 {t|t≤-2或t=0或t≥2}
{t|t≤-2或t=0或t≥2}
◆提炼方法 函数的单调性的判定就是不等式的判定,题(2)中利用单调性把函数值的大小关系转化为自变量的大小关系是最常用的手法,要熟练掌握.
函数的单调性的判定就是不等式的判定,题(2)中利用单调性把函数值的大小关系转化为自变量的大小关系是最常用的手法,要熟练掌握.
[例2]已知奇函数f(x) 在(-∞,0)∪(0,+∞)上有定义,在(0,+∞)上是增函数,f(1)=0,又知函数:
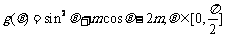
集合
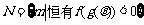 ,求M∩N
,求M∩N
解:f(x)是奇函数, 在(0,+∞)上递增,则f(x) 在(-∞,0)也递增.又由f(1)=0得f(-1)=0.

令t=cosθ则t∈[0,1],又设

要使δ(t)<0,必须使δ(t)在[0,1]内最大值小于零.
10 当
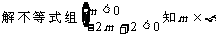

30当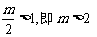 时
时
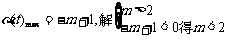
综上: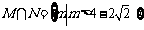
[例3]已知某种商品的定价上涨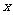 成(1成即为
成(1成即为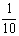 ,
,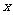 成即为
成即为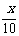 ),其销售量便相应减少
),其销售量便相应减少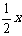 成,按规定,税金是从销售额中按一定的比例缴纳,如果这种商品的定价无论如何变化,从销售额中扣除税金后的金额总比涨价前的销售额少,试求这时税率
成,按规定,税金是从销售额中按一定的比例缴纳,如果这种商品的定价无论如何变化,从销售额中扣除税金后的金额总比涨价前的销售额少,试求这时税率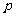 的取值范围(精确到0.1%
)
的取值范围(精确到0.1%
)
解:设原定价为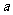 元/件,原销售量为
元/件,原销售量为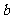 件,则原销售额为
件,则原销售额为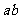 元,由已知得
元,由已知得
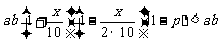 ①
①
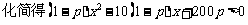
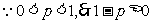
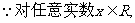 ①式恒成立,
①式恒成立,
∴△<0,解得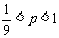 ,故11.1%<
,故11.1%<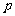 <1,
<1,
即税率的取值范围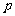 ∈(11.1%,100%).
∈(11.1%,100%).
[例4]设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ(λ<1),画面的上下各留8cm的空白,左右各留5cm的空白,问怎样确定画面的高与宽的尺寸,能使宣传画所用纸张面积最小?如果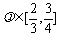 ,那么
,那么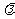 为何值时,能使宣传画所用纸张面积最小?
为何值时,能使宣传画所用纸张面积最小?
解:设画面的高为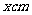 ,宽为
,宽为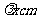 ,则
,则 ,设纸张面积为
,设纸张面积为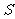 ,则有
,则有
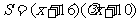
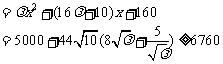 ,
,
当且仅当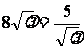 时,即
时,即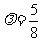 时,
时,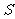 取最小值,此时,高
取最小值,此时,高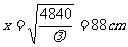 ,
,
宽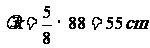 .
.
如果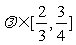 ,则上述等号不能成立.现证函数
,则上述等号不能成立.现证函数
S(λ)在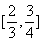 上单调递增.设
上单调递增.设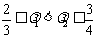 ,
,
则
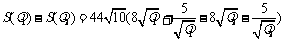
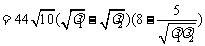
因为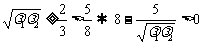 ,
,
又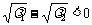 ,
,
所以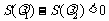 ,故
,故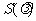 在
在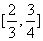 上单调递增,因此对
上单调递增,因此对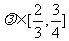 ,当
,当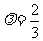 时,
时,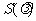 取得最小值.
取得最小值.
◆提炼方法: 用均值不等式求最值时,如果满足“一正二定三相等”,则可直接求解;如果不符合条件中的相等,则应先判断函数的单调性后在求解.
[研讨.欣赏]已知抛物线y=ax2-1上存在关于直线x+y=0成轴对称的两点,试求实数a的取值范围.
解法一:设抛物线上关于直线l对称的两相异点为P(x1,y1)、Q(x2,y2),线段PQ的中点为M(x0,y0),设直线PQ的方程为y=x+b,由于P、Q两点存在,所以方程组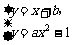 有两组不同的实数解,即得方程
有两组不同的实数解,即得方程
ax2-x-(1+b)=0. ①
判别式Δ=1+4a(1+b)>0. ②
由①得x0=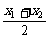 =
=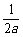 ,y0=x0+b=
,y0=x0+b=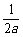 +b.
+b.
∵M∈l,∴0=x0+y0=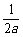 +
+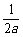 +b,
+b,
即b=-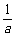 ,代入②解得a>
,代入②解得a>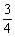 .
.
解法二:设同解法一,由题意得

将①②代入③④,并注意到a≠0,x1-x2≠0,得
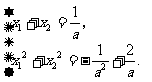
由二元均值不等式易得
2(x12+x22)>(x1+x2)2(x1≠x2).
将⑤⑥代入上式得
2(-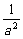 +
+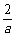 )>(
)>(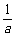 )2,解得a>
)2,解得a>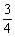 .
.
解法三:同解法二,由①-②,得
y1-y2=a(x1+x2)(x1-x2).
∵x1-x2≠0,∴a(x1+x2)=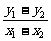 =1.
=1.
∴x0=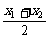 =
=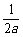 .∵M(x0,y0)∈l,
.∵M(x0,y0)∈l,
∴y0+x0=0,即y0=-x0=-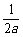 ,从而PQ的中点M的坐标为(
,从而PQ的中点M的坐标为(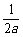 ,-
,-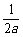 ).
).
∵M在抛物线内部,
∴a(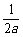 )2-(-
)2-(-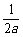 )-1<0.
)-1<0.
解得a>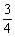 .(舍去a<0,为什么?)
.(舍去a<0,为什么?)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com