
投影
达尔文头像
大家一定还记得恩格斯《在马克思墓前的讲话》一文中,把达尔文发现有机界的发展规律和马克思发现人类历史的发展规律相提并论。一百多年前,达尔文的思想改变了人们对世界的看法,一百多年来,这思想影响了一代又一代的人。作为跨世纪的新一代,你了解达尔文吗?你知道进化论吗?今天我们就一起来打开达尔文进化论之门。
10.某人乘坐出租车从A地到乙地,有两种方案:第一种方案,乘起步价为10元,每km价1.2元的出租车;第二种方案,乘起步价为8元,每km价1.4元的出租车,按出租车管理条例,在起步价内,不同型号的出租车行驶的里路是相等的,则此人从A地到B地选择哪一种方案比较适合?
解:设A地到B地距离为mkm,起步价内行驶的路为akm
显然,当m≤a时,选起步价为8元的出租车比较合适
当m>a时,设m=a+x(x>0),乘坐起步价为10元的出租车费用为P(x)元,乘坐起步价为8元的出租车费用为Q(x)元,则P(x)=10+1.2x,Q(x)=8+1.4x
∵ P(x)-Q(x)=2-0.2x=0.2(10-x)
∴ 当x>10时,P(x)<Q(x),此时起步价为10元的出租车比较合适
当x<10时,P(x)>Q(x),此时选起步价为8元的出租车比较合适
当x=10时,P(x)=Q(x),此时两种出租车任选
[探索题]设关于x的方程2x2-ax-2=0的两根为α、β(α<β),函数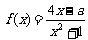 .
.
(Ⅰ)求f (α)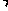 f (β)的值;
f (β)的值;
(Ⅱ)证明f (x)是[α,β]上的增函数;
(Ⅲ)当a为何值时,f (x)在区间[α,β]上的最大值与最小值之差最小?
解:(Ⅰ)由题意知α+β=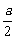 ,α·β=-1,∴α2+β2=
,α·β=-1,∴α2+β2=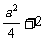 ,
,
f
(α)·f (β)=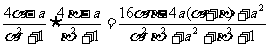
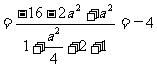 .
.
(Ⅱ)证明:设α≤x1<x2≤β,
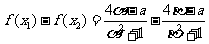
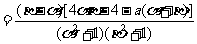
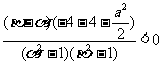
所以f(x)在[α,β]在是增函数.
(法2:导数法)
(Ⅲ)f (x)在区间[α,β]上的最大值f (β)>0,最小值f (α)<0,
又∵| f (α)·f (β) |=4,
∴f
(β)-f (α)=|
f (β)|+| f
(α)|≥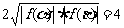
当且仅当| f (β)|=| f (α)|=2时取“=”号,此时f (β)=2,f (α)=-2
∴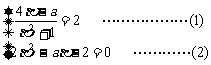
由(1)、(2)得 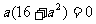 ,∴a=0为所求。
,∴a=0为所求。
9.用一块矩形木板紧贴一墙角围成一直三棱柱空间堆放谷物,已知木板的长为a,宽为b,墙角的两堵墙面和地面两两互相垂直,怎样围法,使直三棱柱的空间最大?这个最大值是多少?
解:如图:A-CC1---B是二墙面所成直二面角, CC1 面ABC
面ABC
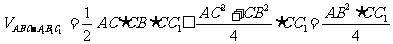 (AC=CB时取”=”)
(AC=CB时取”=”)
当AB=a,AA1=b时,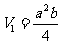
当AB=b,AA1=a时,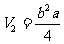
8. (2004全国IV)已知数列{an}的前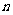 项和Sn满足
项和Sn满足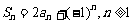 .
.
(1)写出数列{an}的前三项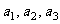 ;
;
(2)求数列{an}的通项公式;
(3)证明:对任意的整数m>4,有
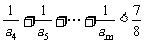 .
.
(Ⅰ)解:由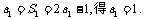
由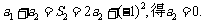
由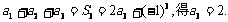
(Ⅱ)解:当 时,有
时,有
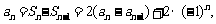

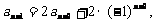 ……
……
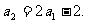 所以
所以

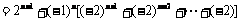
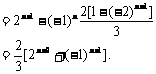
经验证a1也满足上式,所以
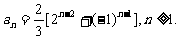
(Ⅲ)证明:
记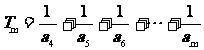

(想用放缩法)
注意到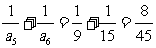
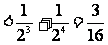 . 一般地
. 一般地
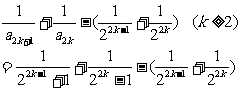
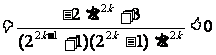
即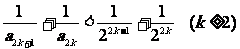
∴当m是奇数时,
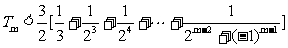
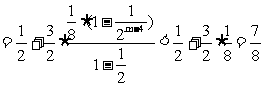
当m是偶数时,再添上第m+1项(放大了)凑够奇数项,利用上述结论可知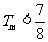 也成立,
也成立,
所以对任意整数m>4,有
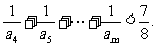
7. (2003福建质检)已知函数f(x)=|log2(x+1)|,实数m、n在其定义域内,且m<n,f(m)=f(n).
求证:(1)m+n>0;
(2)f(m2)<f(m+n)<f(n2).
(1)证法一:由f(m)=f(n),得|log2(m+1)|=|log2(n+1)|,即log2(m+1)=±log2(n+1),
log2(m+1)=log2(n+1), ①
或log2(m+1)=log2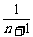 . ②
. ②
由①得m+1=n+1,与m<n矛盾,舍去.
由②得m+1=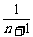 ,即(m+1)(n+1)=1. ③
,即(m+1)(n+1)=1. ③
∴m+1<1<n+1.∴m<0<n.∴mn<0.
由③得mn+m+n=0,m+n=-mn>0.
证法二:(同证法一得)(m+1)(n+1)=1.
∵0<m+1<n+1,∴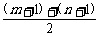 >
>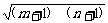 =1.∴m+n+2>2.∴m+n>0.
=1.∴m+n+2>2.∴m+n>0.
(2)证明:当x>0时,f(x)=|log2(x+1)|=log2(x+1)在(0,+∞)上为增函数.
由(1)知m2-(m+n)=m2+mn=m(m+n),且m<0,m+n>0,∴m(m+n)<0.
∴m2-(m+n)<0,0<m2<m+n.
∴f(m2)<f(m+n).
同理,(m+n)-n2=-mn-n2=-n(m+n)<0,
∴0<m+n<n2.∴f(m+n)<f(n2).
∴f(m2)<f(m+n)<f(n2).
6.设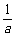 +
+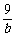 =1,a、b∈N*,则a=
=1,a、b∈N*,则a=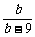 .
.
∴a+b=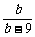 +b,b>9时,
+b,b>9时,
a+b=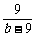 +b-9+10≥16.
+b-9+10≥16.
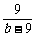 =b-9,即b=12取等号,此时a=4.
=b-9,即b=12取等号,此时a=4.
b<9无解.∴a=4,b=12.答案:4 12
[解答题]
5.x>3或x<1;
3.命题p: ;命题q:a<2.命题p、q一真一假得1<a<2。
;命题q:a<2.命题p、q一真一假得1<a<2。
2.可知当3≤x≤4时,f(x)=-2+x.
当4<x≤5时,f(x)=6-x, 周期是2
故在(-1,0)上增,在(0,1)上减.又由|cos2|<|sin2|,
∴f(cos2)>f(sin2)
6.在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小,1=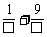 .
.
◆简答提示:1-4.ADCD; 1. 易证M>4,N≤4<M.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com