
3、(辽宁省大连市第二十四中学2009届高三高考模拟)设O为平行四边形ABCD的对称中心,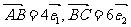 ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.
答案:B
2、(江西省崇仁一中2009届高三第四次月考)给出下面四个命题:
①对于任意向量a、b,都有|a·b|≥a·b成立;
②对于任意向量a、b,若a2=b2,则a=b或a= -b;
③对于任意向量a、b、c,都有a·(b·c)=(b·c)·a成立;
④对于任意向量a、b、c,都有a·(b·c)=(b·a)·c成立.
其中错误的命题共有( )
A.1个 B.2个 C.3个 D.4个
答案:B
1、(四川省成都市高2009届高中毕业班第一次诊断性检测)已知点O为△ABC内一点,且+2+3=,则△AOB、△AOC、△BOC的面积之比等于 A、9∶4∶1 B、1∶4∶9 C、3∶2∶1 D、1∶2∶3 答案:C
28、(山西省实验中学高三年级第四次月考)设 ,其中a、b为正的常数,实数x>1,如果总有
,其中a、b为正的常数,实数x>1,如果总有 的大小。(要有具体推导过程)
的大小。(要有具体推导过程)
解: , …………2分
, …………2分
 …………8分
…………8分
 …………12分
…………12分
27、(湖北省黄冈市高三年级期末考试)在平面直角坐标系中,O为坐标原点,已知向量 ,又点
,又点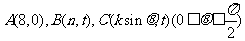
(1)若 且
且 ,求向量
,求向量 ;
;
(2)若向量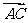 与向量
与向量 共线,当
共线,当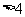 时,且
时,且 取最大值为4时,求
取最大值为4时,求
解: 
又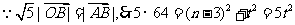 ,得
,得 (4分)
(4分)
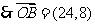 或
或

 与
与 向量共线,
向量共线, 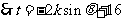
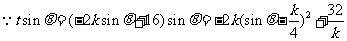
 ,
, 当
当 时,
时, 取最大值为
取最大值为 (8分)
(8分)
由 ,得
,得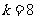 ,此时
,此时
 (12分)
(12分)
26、(山东省博兴二中高三第三次月考)已知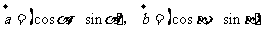 ,其中
,其中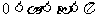 。
。
(1)求证: 与
与 互相垂直;
互相垂直;
(2)若 与
与 (
(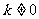 )的长度相等,求
)的长度相等,求 。
。
解析:(1)因为
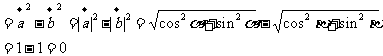
所以 与
与 互相垂直。
互相垂直。
(2) ,
,
 ,
,
所以 ,
,
 ,
,
因为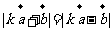 ,
,
所以 ,
,
有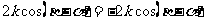 ,
,
因为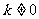 ,故
,故 ,
,
又因为 ,
,
所以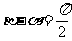 。
。
25、(北京市丰台区高三统一练习一)已知 ,
,  ,
, ,
, .
.
(Ⅰ)当 时,求使不等式
时,求使不等式 成立的x的取值范围;
成立的x的取值范围;
(Ⅱ)求使不等式 成立的x的取值范围.
成立的x的取值范围.
解:(Ⅰ)当 时,
时, ,
, .
.
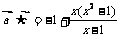
 . ……………………………………… 2分
. ……………………………………… 2分
∵  ,
,
∴  解得
解得
 或
或 .
.
∴ 当 时,使不等式
时,使不等式 成立的x的取值范围是
成立的x的取值范围是
 .…………………………………………… 5分
.…………………………………………… 5分
(Ⅱ)∵  ,…… 8分
,…… 8分
∴ 当m<0时, ;
;
当m=0时, 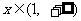 ;
;
当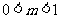 时,
时, ;
;
当m=1时, ;
;
当m>1时, .
.
24、(四川省巴蜀联盟高三年级第二次联考)设向量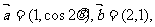
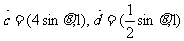 ,其中
,其中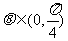 .
.
(1)求 的取值范围;
的取值范围;
(2)若函数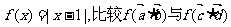 的大小
的大小
解:(1)∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,∴
,∴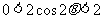 ,
,
∴ 。
。
(2)∵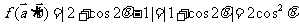 ,
,
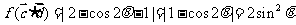 ,
,
∴ ,
,
∵ ,∴
,∴ ,∴
,∴ ,∴
,∴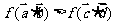
23、(2008学年第一学期期中杭州七校高三联考数学试题)
已知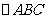 的面积满足
的面积满足 ,且
,且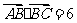 ,
, 与
与 的夹角为
的夹角为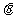 。
。
(1)求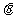 的取值范围;
的取值范围;
(2)求函数 的最小值。
的最小值。
解:(1)由题意知:

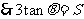 …………………4分
…………………4分
又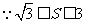
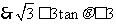 即
即
又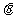 为
为 与
与 的夹角,所以
的夹角,所以 ……7分
……7分
(2)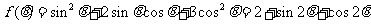
 …………10分
…………10分
由 ,知
,知 ……………13分
……………13分
∴当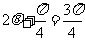 ,即
,即 时,
时, ………………14分
………………14分
22、(温州市十校2008学年高三第一学期期初联考 数学试题(文)) 已知A、B、C三点的坐标分别为 、
、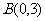 、
、
(1)若 的值;
的值;
(2)若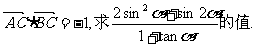
解:(1)


∵ ∴
∴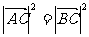
即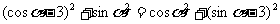
∴ (4分)
(4分)
又∵
∴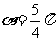 (7分)
(7分)
(2)
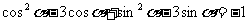
∴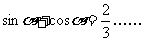 ①
①
① 平方,得 (10分)
(10分)

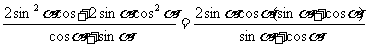
= (14分)
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com