
11、(山西省太原五中2008-2009学年度高三上学期10月月考)已知集合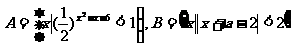 ,若
,若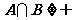 ,求实数
,求实数 的取值范围。
的取值范围。
解:(略)答案:(-∞,1)∪(2,+∞)
10、(江西省崇仁一中2009届高三第四次月考)已知函数f(x)=log2(x+-a)的定义域为A,值域为B.
(1)当a=4时,求集合A;
(2)设I=R为全集,集合M={x|y=},若(CIM)∪(CIB)=,求实数a的取值范围.
解:(1)当a=4时,由x+-4==>0,
解得0<x<1或x>3, 故A={x|0<x<1或x>3}………………6分
(2)由(CIM)∪(CIB)=,得CIM=,且CIB=,即M=B=R,………8分
若B=R,只要u=x+-a可取到一切正实数,则x>0及umin≤0,∴umin=2-a≤0,
解得a≥2……①………10分
若M=R,则a=5或 解得1<a≤5……②
由①②得实数a的取值范围为[2,5]……………………12分
9、(本大题满分10分)(广东省深圳中学2008-2009学年度高三第一学段考试)已知集合 ,全集为实数集R。
,全集为实数集R。
(1)求 ;
;
(2)如果 的取值范围。
的取值范围。
解:(1)

 ……………………5分
……………………5分
(2)如图
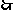 当a>3时,A
当a>3时,A
本题重点考查集合的运算及数形结合的思想。
8、(安徽省潜山县三环中学2009届高三上学期第三次联考)函数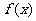 =
= 的定义域为集合A,函数
的定义域为集合A,函数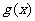 =
=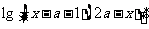 的定义域为集合B,若B
的定义域为集合B,若B A,求实数
A,求实数 的取值范围。
的取值范围。
解:由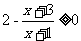 且
且
可得 A={ x<-1或x≥1}
x<-1或x≥1}
又 B={ (x-a-1)(x-2a)< 0}
(x-a-1)(x-2a)< 0}
 ∵φ≠B
∵φ≠B A,
A,
∴①
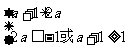 ∴a>1
∴a>1
或②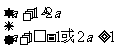 ∴a≤-2或
∴a≤-2或 ≤a<1;
≤a<1;
∴a>1或a≤-2或 ≤a<1;
≤a<1;
7、(江苏运河中学2009年高三第一次质量检测)已知集合 ,
,
(1)若 ,求实数m的值;
,求实数m的值;
(2)设全集为R,若 ,求实数m的取值范围。
,求实数m的取值范围。
解:(Ⅰ)∵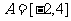 ,
, 
 ,
,
∴  ∴
∴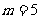
(Ⅱ) 
∵ ∴
∴ , ∴
, ∴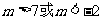
6、(江西省南昌二中2008-2009学年度第一轮第二次段考)已知命题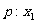 和
和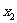 是方程
是方程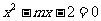 的两个实根,不等式
的两个实根,不等式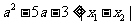 对任意实数
对任意实数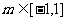 恒成立;命题
恒成立;命题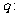 不等式
不等式 有解;若命题
有解;若命题 是真命题,命题
是真命题,命题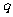 是假命题,求
是假命题,求 的取值范围.
的取值范围.
解: 、
、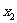 是方程
是方程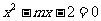 的两个实根
的两个实根
 ,
,  ,∴当
,∴当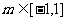 时,
时,
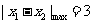 ,由不等式
,由不等式 对任意实数
对任意实数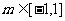 恒成立可得:
恒成立可得:
 ,
,  或
或 ,∴命题
,∴命题 为真命题时
为真命题时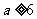 或
或 ;
;
命题 不等式
不等式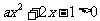 有解,①当
有解,①当 时,显然有解;②当
时,显然有解;②当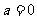 时,
时, 有解;③当
有解;③当 时,
时, 有解,
有解, ,
,
从而命题 不等式
不等式 有解时
有解时 。 又命题
。 又命题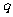 是假命题,
是假命题, 。
。
5、(河南省实验中学2008-2009学年高三第二次月考)已知集合A={ },B=
},B= ,C=
,C= ,若
,若 与
与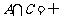 同时成立,求实数a的值。
同时成立,求实数a的值。
解:易求得B= ,C=
,C=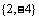 ,由
,由 知A与B的交集为非空集。
知A与B的交集为非空集。
故2,3两数中至少有一适合方程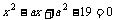
又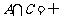 ,∴
,∴ ,即
,即 得,a=5或a=-2
得,a=5或a=-2
当a=5时,A= ,于是
,于是 ,故a=5舍去。
,故a=5舍去。
当a=-2时,A=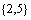 ,于是
,于是 ,∴a=-2。
,∴a=-2。
4、(福建省莆田第一中学2008-2009学年度上学期第一学段段考)设P:关于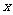 的不等式
的不等式 的解集为实数集R,
的解集为实数集R,
Q:不等式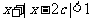 在实数集R上有解,
在实数集R上有解,
如果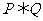 为真,
为真, 为假,求
为假,求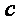 的取值范围.
的取值范围.
解:关于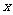 的不等式
的不等式 的解集为R,
的解集为R,
则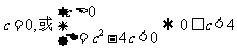 4分
4分
不等式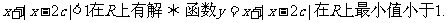

 为
为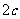
 10分
10分
如果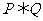 为真,
为真, 为假,则C的取值范围为
为假,则C的取值范围为 。 12分
。 12分
3、(福建省福州三中高三年级第二次月考)已知集合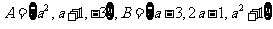 ,若
,若 ,
,
求实数 的值。
的值。
解:∵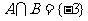
∴ ……………………2分
……………………2分
∵
∴ 即a=0或-1………………6分
即a=0或-1………………6分
①当a=0时,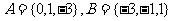
此时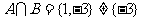 ,舍去………………9分
,舍去………………9分
②当a=-1时,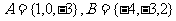
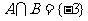 ,合题意………………10分
,合题意………………10分
∴由①②可知 为所求 ……………………12分
为所求 ……………………12分
2、(上海市张堰中学高2009届第一学期期中考试)已知集合 ,集合
,集合 ,不等式
,不等式 的解集为
的解集为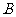 ,若
,若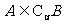 ,求实数
,求实数 的取值范围.
的取值范围.
解:


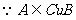

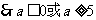
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com