
1.下列各物体,哪个是绝对黑体?
A.不辐射可见光的物体
B.不辐射任何光线的物体;
C.不能反射可见光的物体
D.不能反射任何光线的物体.
1922、1923年康普顿及其学生吴有顺进行了系统研究
(2)实验装置:如图
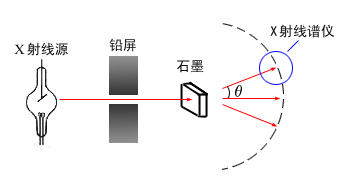
(3)实验结果:
a.散射光中除有与入射线波长 相同的,还有比
相同的,还有比 大的波长
大的波长 ,
, 随散射角
随散射角 而异,
而异, 增大时,
增大时, 的强度增加,
的强度增加, 的强度减小.
的强度减小.
b.当散射角 确定时,波长的增加量
确定时,波长的增加量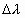 与散射物质的性质无关.
与散射物质的性质无关.
c.康普顿散射的强度与散射物质有关.原子量小的散射物质,康普顿散射较强,原波长的谱线强度较低.反之相反.
按经典电磁理论,光的散射是带电粒子在入射光电场作用下作受迫振动,散射光与入射光应该有相同波长.
按照光子理论,一个光子与散射物中的一个自由电子发生碰撞,散射光子将沿某一方向进行--康普顿散射,光子与电子之间碰撞遵守能量守恒和动量守恒,电子受到反冲而获得一定的动量和动能,因此散射光子能量要小于入射光子能量.由光子的能量与频率间的关系 可知,散射光的频率要比入射光的频率低,因此散射光的波长
可知,散射光的频率要比入射光的频率低,因此散射光的波长 .如果入射光子与原子中被束缚得很紧的电子碰撞,光子将与整个原子作弹性碰撞(如乒乓球碰铅球),散射光子的能量就不会显著地减小,所以观察到的散射光波长就与入射光波长相同.
.如果入射光子与原子中被束缚得很紧的电子碰撞,光子将与整个原子作弹性碰撞(如乒乓球碰铅球),散射光子的能量就不会显著地减小,所以观察到的散射光波长就与入射光波长相同.
下图为光子与自由电子弹性碰撞的示意图.应用相对论质量、能量、动量关系,有

式中m0、m为电子的静质量和质量, .将上式第二式写成分量式
.将上式第二式写成分量式


解以上联立方程组,消去 ,即得
,即得

式中
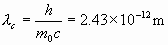
叫做电子的康普顿波长.上式表明 与散射物质的性质无关.
与散射物质的性质无关.
康普顿散射进一步证实了光子论,证明了光子能量、动量表示式的正确性,光确实具有波粒两象性.另外证明在光电相互作用的过程中严格遵守能量、动量守恒定律.
在基元相互作用过程中,能量、动量守恒.1927年,康普顿因此获诺贝尔物理学奖
[例1]求 的可见光光子和
的可见光光子和 的X射线光子的能量、动量和质量?
的X射线光子的能量、动量和质量?
 ,
, ,
,
 ,
, ,
,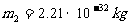
[例2] 的X射线,射向静止的自由电子,观察方向
的X射线,射向静止的自由电子,观察方向 ,求:①
,求:①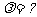 ②反冲电子的动能和动量?
②反冲电子的动能和动量?
(①
② ,
, 
或: )
)
[例3]已知X光光子的能量为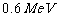 ,在康普顿散射之后,波长变化了20%,求反冲电子的能量.(
,在康普顿散射之后,波长变化了20%,求反冲电子的能量.( )
)
练习
5.康普顿效应
(1)散射现象:光通过不均匀物质时,向各个方向发射的现象
实验发现:X射线→金属或石墨时,也有散射现象
4.光子的质量和动量

光子既具有一定的能量,就必须具有质量.但是光子以光的速度运动,牛顿力学便不适用.按照狭义相对论质量和能量的关系式  ,就可以决定一个光子的质量
,就可以决定一个光子的质量
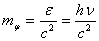
在狭义相对论中,质量和速度的关系为

m0为静止质量,光子永远以不变的速度c运动,因而光子的静止质量必然等于零,否则m将为无穷大.因为相对于光子静止的参照系是不存在的,所以光子的静止质量等于零也是合理的.而原子组成的一般物质的速度总是远小于光速的,故它们的静止质量不等于零.在m0是否等于零这一点上光子和普通的物质有显著的区别.在狭义相对论中,任何物体的能量和动量的关系为

光子的静止质量为0,故光子的动量为
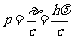
这是和光子的质量为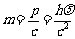 ,速度为c.
,速度为c.
光电效应明确了光的行为像粒子,并且可用动力学的变量(动量和能量)来描述粒子的行为; 在光和物质相互作用过程中,光子是整体在起作用.另一方面,在讨论衍射和干涉现象时,需要把光作为波动来处理,于是用波长来阐明问题.
波动特征和粒子特征是互相对立的,但并不是矛盾的.
光的波长既适宜于显示波动特征,同时又也容易显示粒子特征.对于电磁波谱的长波段,表示其波动特征的物理量T和较大,而表示其粒子特征的物理量ε和p 较小,因而容易显示波动特征,反之,对于电磁波谱的短波段,表示其波动特征的物理量T和 较小,而表示其粒子特征的物理量ε和p较大,因而容易显示粒子特征.
[例1]将一块金属板放在离单色点光源5米远的地方,光源的光功率输出为10-3瓦.假设被打出的光电子可以从半径为10-8米(约相当于原子直径的十倍)的圆面上以从光源取得它所得的能量,已知打出一个电子需要5.0eV.现在将光认为是经典波动,对这种装置的一个“靶”来说,打出一个光电子需要多长时间?
[解析]电子接受能量的靶面积为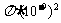 ,半径为5米的球面面积为
,半径为5米的球面面积为  ,前者是后者的
,前者是后者的  ,故每秒投射于靶面积上的能量为
,故每秒投射于靶面积上的能量为
 焦耳.
焦耳.
打出一个电子需要能量5eV,即  焦耳,故积累这些能量需时
焦耳,故积累这些能量需时
 秒=22.22小时.
秒=22.22小时.
实际上光电效应是几时的,根本不需要这么长的时间.这说明光与光电阴极电子的作用决不是经典波动模型中能量积累的那种形式
[例2]若-个光子的能量等于一个电子的静能量,试问该光子的动量和波长是多少?在电磁波谱中它是属何种射线?
[解析]-个电子的静能量为m0c2,按题意
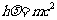
光子的动量

光子的波长

因电磁波谱中γ射线的波长在300~10-4 范围内,所以该光子在电磁波谱中属于γ射线.
范围内,所以该光子在电磁波谱中属于γ射线.
3.爱因斯坦光电效应方程
为了解释光电效应的所有实验结果,1905年爱因斯坦推广了普朗克关于能量子的概念.前面已经指出普朗克在处理黑体辐射问题时,只是把器壁的振子能量量子化,腔壁内部的辐射场仍然看作是电磁波.然而爱因斯坦在光电效应的研究中指出:光在传播过程中具有波动的特性,而在光和物质相互作用的过程中,光能量是集中在一些叫做光量子(简称光子)的粒子上.从光子的观点来看,产生光电效应的光是光子流,单个光子的能量与频率成正比即:
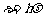

式中h是普朗克常数.
把光子的概念应用于光电效应时,爱因斯坦还认为一个光子的能量是传递给金属中的单个电子的.电子吸收一个光子后,把能量的一部分用来挣脱金属对它的束缚,余下的一部分就变成电子离开金属表面后的动能,按能量守恒和转换定律应有:


上式称为爱因斯坦光电效应方程.其中 为光电子的动能,W为光电子逸出金属表面所需的最小能量,称为脱出功.
为光电子的动能,W为光电子逸出金属表面所需的最小能量,称为脱出功.
对光电效应四个定律的解释:
(1)光电效应第一定律的解释
 :光子数
:光子数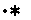 光电子数
光电子数
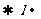

(2)光电效应第二定律的解释:



 :遏止电压,
:遏止电压,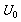 :逸出电位
:逸出电位
(3)光电效应第三定律的解释:


光电子动能不小于零
(4)光电效应第四定律的解释:
 :光子能量
:光子能量 电子,无须能量积累时间
电子,无须能量积累时间
1921年,爱因斯坦因对物理学的贡献,特别是光电效应获诺贝尔物理学奖
爱因斯坦理论的验证
1916年,密立根进行了精密的测量,证明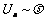 确为直线,且直线的斜率为
确为直线,且直线的斜率为 .1923年获诺贝尔物理学奖
.1923年获诺贝尔物理学奖
2.光电效应和波动理论的矛盾
光能使金属中的电子释放,从经典理论来看,是不难理解的.我们知道金属里面有大量的自由电子,这些电子通常受到正电荷的引力作用,而被束缚在金属表面以内,它们没有足够的能量逸出金属表面.但因光是电磁波,在它的照射下,光波中的电场作用于电子,迫使电子振动,给电子以能量,使电子有足够的能力挣脱金属的束缚而释放出去.因此按照光的电磁理论可以预测:
(1)光愈强,电子接受的能量愈多,释放出去的电子的动能也愈大.
(2)释放电子主要决定于光强,应当与频率等没有关系.但是,实验测量的结果却并不如此.
(3)关于光照的时间问题,波动观点更是陷于困境.从波动观点来看,光能量是均匀分布,在它传播的空间内,由于电子截面很小,积累足够能量而释放出来必须要经过较长的时间,合实验事实完全完全不符.
4.光的照射和光电子的释放几乎是同时的,在测量的精度范围内10-9s观察不出这两者间存在滞后现象.
3.入射光的频率低于遏止频率(极限频率,红限频率)的光,不论光的强度如何,照射时间多长,都没光电子发射.(光电效应第三定律)
2.光电子的最大初动能(或遏止电压)与入射光的强度无关,而只与入射光的频率有关.频率越大,光电子的能量就越大.(光电效应第二定律)
1.饱和电流I的大小与入射光的强度成正比,也就是单位时间内被击出的光电子数目与入射光的强度成正比.(光电效应第一定律)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com