
8. (2008深圳调研文)甲、乙两人各抛掷一次正方体骰子(它们的六个面分别标有数字 ),设甲、乙所抛掷骰子朝上的面的点数分别为
),设甲、乙所抛掷骰子朝上的面的点数分别为 、
、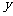 ,则满足复数
,则满足复数 的实部大于虚部的概率是( )
的实部大于虚部的概率是( )
A. B.
B. C.
C. D.
D.
7.(2008广州一模理)在区间 上任取两个数
上任取两个数 ,方程
,方程
的两根均为实数的概率为( )
A. B.
B. C.
C. D.
D.
6. (2008佛山一模理)如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( )
(2008佛山一模理)如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( )
A.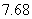 B.
B. C.
C.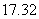 D.
D.
5. (2007韶关二模文) 一个停车场有3个并排的车位,分别停放着“红旗”,“捷达”,“桑塔纳”轿车各一辆,则“捷达””车停在“桑塔纳”车的右边的概率和“红旗”车停在最左边的概率分别是( )
A.  ,
,
 .
.  ,
,
 .
.  ,
,
 .
.  ,
,
4.(2007韶关一模文)有3张奖券,其中2张可中奖,现3个人按顺序依次从中抽一张,小明最后抽,
则他抽到中奖券的概率是( )
(A) (B)
(B) (C)
(C) (D)
(D)
3.( 2005年广东)先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有1,2,3,4,5,6),
骰子朝上的面的点数分别为x,y,则使  的概率为( )
的概率为( )
A. B.
B. C.
C.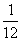 D.
D.
2.(2008惠州调研二理)方程 有实根的概率为(
).
有实根的概率为(
).
A、 B、
B、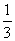 C、
C、 D、
D、
1.(2008辽宁文、理) 4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A. B.
B. C.
C. D.
D.
5.不确定关系的应用
(1)估算氢原子可能具有的最低能量
电子束缚在半径为r的球内,所以

当不计核的运动,氢原子的能量就是电子的能量:

用不确定关系代入上式得:

基态能应满足
 得
得

由此得出基态氢原子半径

基态氢原子的能量

与波尔理论结果一致。
(2) 解释谱线的自然宽度
原子中某激发态的平均寿命为
由普朗克能量子假说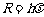 及
及

这就是谱线的自然宽度。

[例1]已知一个光子沿 方向传播,其波长
方向传播,其波长 ,对波长的测量是相当准确的,
,对波长的测量是相当准确的, ,求该光子
,求该光子 坐标的不确定度;
坐标的不确定度;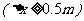
[例2]质量为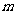 的粒子位置的不确定量等于粒子的德布罗意波长
的粒子位置的不确定量等于粒子的德布罗意波长 ,求
,求 的最小值.
的最小值.
[例3]氢原子中基态电子的速度大约是 ,电子位置的不确定度可按原子大小估算
,电子位置的不确定度可按原子大小估算 ,求电子速度的不确定度.
,求电子速度的不确定度.
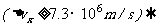 轨道概念在量子力学中无意义!
轨道概念在量子力学中无意义!
4.其它表示:
能量、时间:
角动量、角位移:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com