
3. 现代类人猿和人类的共同祖先是 ( )
(A) 长臂猿 (B) 黑猩猩 (C) 森林古猿 (D) 大猩猩
2. 严重干旱可能造成作物颗粒无收,从光合作用的角度来看,这表明光合作用的必要条件(或重要原料)是 ( )
(A) 光 (B) 水 (C) 二氧化碳 (D) 适宜温度
1. 绿色植物的光合作用为地球生物提供了 ( )
①食物来源 ②空气来源 ③氧气来源 ④能量来源
(A) ①②③ (B) ②③④ (C) ①②④ (D) ①③④
20.(16分)设(2-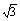 x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:
x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:
(1)a0;
(2)a1+a2+…+a100;
(3)a1+a3+a5+…+a99;
(4)(a0+a2+…+a100)2-(a1+a3+…+a99)2.
解 (1)由(2-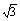 x)100展开式中的常数项为C
x)100展开式中的常数项为C ·2100,
·2100,
即a0=2100,或令x=0,则展开式可化为a0=2100.
(2)令x=1,可得
a0+a1+a2+…+a100=(2-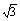 )100. ①
)100. ①
∴a1+a2+…+a100=(2-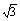 )100-2100.
)100-2100.
(3)令x=-1可得
a0-a1+a2-a3+…+a100=(2+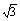 )100. ②
)100. ②
与x=1所得到的①联立相减可得,
a1+a3+…+a99= .
.
(4)原式=[(a0+a2+…+a100)+(a1+a3+…+a99)]×[(a0+a2+…+a100)-(a1+a3+…+a99)]
=(a0+a1+a2+…+a100)(a0-a1+a2-a3+…+a98-a99+a100)
=(2-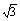 )100·(2+
)100·(2+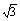 )100=1.
)100=1.
19.(16分)已知(a2+1)n展开式中的各项系数之和等于(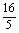 x2+
x2+ )5的展开式的常数项,而(a2+1)n的展开式的系数最大的项等于54,求a的值(a∈R).
)5的展开式的常数项,而(a2+1)n的展开式的系数最大的项等于54,求a的值(a∈R).
解 (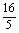 x2+
x2+ )5的通项公式为
)5的通项公式为
Tr+1=C
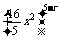 ·
·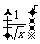 =C
=C ·
· ·x
·x
令20-5r=0,则r=4,∴常数项为T5=C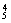 ×
×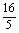 =16.
=16.
又(a2+1)n展开式的各项系数之和为2n,依题意得2n=16,
n=4,由二项式系数的性质知(a2+1)4展开式中系数最大的项是中间项T3,所以C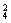 (a2)2=54,即a4=9,所以a=±
(a2)2=54,即a4=9,所以a=±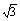 .
.
18.(16分)4个不同的红球和6个不同的白球放入同一个袋中,现从中取出4个球.
(1)若取出的红球的个数不少于白球的个数,则有多少种不同的取法?
(2)取出一个红球记2分,取出一个白球记1分,若取出4个球总分不少于5分,则有多少种不同的取法?
解 (1)依题意可知,取出的4个球中至少有2个红球,可分为三类:
①全取出红球,有C 种不同的取法;②取出的4个球中有3个红球1个白球,有C
种不同的取法;②取出的4个球中有3个红球1个白球,有C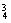 ×C
×C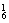 种取法;
种取法;
③取出的4个球中有2个红球2个白球,有C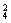 ×C
×C 种不同的取法.
种不同的取法.
由分类计数原理知,共有C +C
+C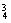 ×C
×C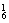 + C
+ C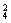 ×C
×C =115种不同的取法.
=115种不同的取法.
(2)依题意知,取出的4个球中至少要有1个红球,从红白10个球中取出4个球,有C 种不同的取法,而全是白球的取法有C
种不同的取法,而全是白球的取法有C 种,从而满足题意的取法有:C
种,从而满足题意的取法有:C -C
-C =195(种).
=195(种).
17.(14分)已知在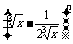 的展开式中,第6项为常数项.
的展开式中,第6项为常数项.
(1)求n;
(2)求含x2的项的系数;
(3)求展开式中所有的有理项.
解 (1)通项公式为Tr+1=C x
x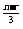
 x
x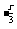
=C
 x
x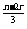 ,
,
因为第6项为常数项,所以r=5时,
有 =0,即n=10.
=0,即n=10.
(2)令 =2,得r=
=2,得r=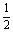 (n-6)=2,
(n-6)=2,
∴所求的系数为C
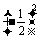 =
=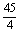 .
.
(3)根据通项公式,由题意得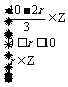
令 =k (k∈Z),则10-2r=3k,即r=5-
=k (k∈Z),则10-2r=3k,即r=5- k,
k,
∵r∈Z,∴k应为偶数.
∴k可取2,0,-2,即r可取2,5,8.
所以第3项,第6项与第9项为有理项,它们分别为
T3= ,T6=
,T6= ,T9=
,T9= .
.
16.(14分)五位老师和五名学生站成一排:
(1)五名学生必须排在一起共有多少种排法?
(2)五名学生不能相邻共有多少种排法?
(3)老师和学生相间隔共有多少种排法?
解 (1)捆绑法共有A ·A
·A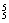 =86 400种排法.
=86 400种排法.
(2)插空法共有A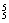 ·A
·A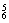 =86 400种排法.
=86 400种排法.
(3)排列方式只能有两类,如图所示:
○□○□○□○□○□
□○□○□○□○□○
(用□表示老师所在位置,用○表示学生所在位置)
故有2A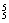 ·A
·A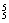 =28 800种排法.
=28 800种排法.
15.(14分)二次函数y=ax2+bx+c的系数a、b、c,在集合{-3,-2,-1,0,1,2,3,4}中选取3个不同的值,则可确定坐标原点在抛物线内部的抛物线多少条?
解 由图形特征分析,a>0,开口向上,坐标原点在内部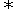 f(0)=c<0;a<0,开口向下,原点在内部
f(0)=c<0;a<0,开口向下,原点在内部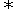 f(0)=c>0,
f(0)=c>0,
所以,对于抛物线y=ax2+bx+c来讲,原点在其内部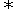 af(0)=ac<0,则确定抛物线时,可先定一正一负的a和c,再确定b,故满足题设的抛物线共有C
af(0)=ac<0,则确定抛物线时,可先定一正一负的a和c,再确定b,故满足题设的抛物线共有C C
C A
A A
A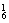 =144(条).
=144(条).
14.(ax- )8的展开式中x2的系数是70,则实数a的值为
.
)8的展开式中x2的系数是70,则实数a的值为
.
答案 ±1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com