1、设有如下三个命题：①底面是平行四边形的四棱柱是平行六面体；②底面是矩形的平行六面体是长方体；③直四棱柱是直平行六面体。其中真命题的个数是(　 )

A、0　　　　　　 B、1　　　　　 C、2　　　　　　　 D、3

例1、如图，已知正三棱柱ABC-A₁B₁C₁的底面边长为6，B₁C＝10，D为AC的中点E、F分别在侧棱A₁A和BB₁上,且AF＝2BE＝BC．

(1)求证：AB₁∥平面C₁BD；

(2)求异面直线AB₁和BC₁所成的角；

(3)求直线AB₁到平面C₁BD的距离

(4)求过F、E、C的平面与棱柱下底面所成二面角的大小．

例2、如图．已知斜三棱柱ABC-A₁B₁C₁中，AC＝BC、D为AB的中点，平面ABC⊥平面ABB₁A₁，异面直线BC₁与AB₁互相垂直．

(1)求证：AB₁⊥CD；

(2)求证：AB₁⊥平面A₁CD；

(3)若AB₁＝5，求点A到平面A₁CD的距离．

例3如图正三棱柱ABC－A₁B₁C₁的各棱均相等，D是BC上的一点，AD⊥C₁D

(1)求证：面ADC₁⊥侧面BCC₁B₁

(2)求二面角C－AC₁－D的大小(用反正弦表示)；

(3)若AB=2，求直线A₁B与截面ADC₁之间的距离

例4.如图，直三棱柱ABC-A₁B₁C₁中，底面是等腰直角三角形，∠ACB＝90°，侧棱AA₁＝2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的垂心G.

　 (1)求A₁B与平面ABD所成角的大小(结果用反三角函数值表示)；

　 (2)求点A₁到平面AED的距离.

4、一个长方体共一顶点的三个面的面积分别为、、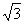，这个长方体对角线的长是…(　)

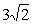(A)　　　　　　 (B)　　 　　　　(C)6　　　　　　 (D)

3、在直三棱柱ABC－A₁B₁C₁中，AA₁＝AB＝AC，AB⊥AC，M是CC₁的中点，Q是BC的中点,在A₁B₁上,则直线PQ与直线AM所成的角为______.

2、一个长方体的全面积是22，体积为8，则这样的长方体…………………………………………( 　　)

(A)有一个　　　　　　　　　　　　　 (B)有两个

(C)有无数多个　　　　　　　　　　　 (D)不存在

1、棱柱成为直棱柱的一个必要而不充分条件是…………………………………………………(　　 ).

(A)它的一条侧棱垂直于底面　　　　　 (B)它的一条侧棱与底面两条边垂直

(C)它的一个侧面与底面都是矩形　　　 (D)它的一个侧面与底面的一条边垂直

1. 棱柱.

⑴①直棱柱侧面积：(为底面周长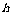，是高)该公式是利用直棱柱的侧面展开图为矩形得出的.

②斜棱住侧面积：(是斜棱柱直截面周长，是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.

⑵{四棱柱}{平行六面体}{直平行六面体}{长方体}{正四棱柱}{正方体}.

{直四棱柱}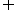{平行六面体}={直平行六面体}.

⑶棱柱具有的性质：

①棱柱的各个侧面都是平行四边形，所有的侧棱都相等；直棱柱的各个侧面都是矩形；正棱柱的各个侧面都是全等的矩形.

②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形.

③过棱柱不相邻的两条侧棱的截面都是平行四边形.

注：①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×)

(直棱柱不能保证底面是钜形可如图)

②(直棱柱定义)棱柱有一条侧棱和底面垂直.

⑷平行六面体：

定理一：平行六面体的对角线交于一点，并且在交点处互相平分.

[注]：四棱柱的对角线不一定相交于一点.

定理二：长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.

推论一：长方体一条对角线与同一个顶点的三条棱所成的角为，则.

推论二：长方体一条对角线与同一个顶点的三各侧面所成的角为，则.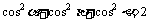

[注]： ①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形)

②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直棱柱才行)

③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等，推不出底面为矩形)

④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交，可能不相交，若两条边相交，则应是充要条件)

10. 设、b是满足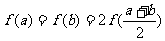的实数，其中.

　 ⑴求证：；　　　 ⑵求证：.

解：(1)由只能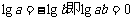

(2)由

由于a、b为正数，

，

即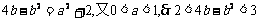

[探索题]已知，求证：

(1) 中至少有一个不小于。

(2) 若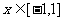时， ,求证：|p|≤1.

[分析]由于题(1)的结论是：三个函数值中“至少有一个不小于”，情况较复杂，会出现多个异向不等式组成的不等式组，一一证明十分繁冗，而结论的反面构成三个同向不等式，结构简单，故采用反证法为宜。

证明(1)(反证法)假设都小于，则

，

而

，相互矛盾

∴中至少有一个不小于。

(2)由已知得，

∴∴

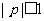
9.已知f(x)=x²－x+c定义在区间［0，1］上，x₁、x₂∈［0，1］，且x₁≠x₂，求证：

(1)f(0)=f(1)；

(2)| f(x₂)－f(x₁)|＜|x₁－x₂|；

(3)| f(x₁)－f(x₂)|＜；

(4)| f(x₁)－f(x₂)|≤.

证明：(1)f(0)=c，f(1)=c，

∴f(0)=f(1).

(2)| f(x₂)－f(x₁)|=|x₂－x₁||x₂+x₁－1|.

∵0≤x₁≤1，∴0≤x₂≤1，0＜x₁+x₂＜2(x₁≠x₂).

∴－1＜x₁+x₂－1＜1.

∴| f(x₂)－f(x₁)|＜|x₂－x₁|.

(3)不妨设x₂＞x₁，由(2)知

| f(x₂)－f(x₁)|＜x₂－x₁.　　　　　　　　　　　　　　 ①

而由f(0)=f(1)，从而

| f(x₂)－f(x₁)|=| f(x₂)－f(1)+f(0)－f(x₁)|

≤| f(x₂)－f(1)|+| f(0)－f(x₁)|＜|1－x₂|+|x₁|＜1－x₂+x₁.　　　 ②

①+②得2| f(x₂)－f(x₁)|＜1，

即| f(x₂)－f(x₁)|＜.

(4)|f(x₂)－f(x₁)|≤f_max－f_min=f(0)－f()=.

8.求证：(1)≤+.

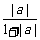(2) 如果设m等于，和1中最大的一个，时，则.

　证明(1)：令f(x)=(x≥0)，易证f(x)在［0，+∞)上单调递增.

|a+b|≤|a|+|b|，

∴f(|a+b|)≤f(|a|+|b|)，

即≤=≤.

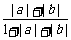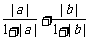法2:分析法

当|a+b|=0时，不等式成立；

当|a+b|≠0时，原不等式即为≤.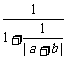

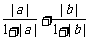∵|a+b|≤|a|+|b|,

∴左边

(2)(综合法)由已知得，，，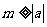

从而知,