1．某班有50人，其中三好学生10人，优秀学生干部5人，在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是 (　　　 ) 　A．720，360 　　　　　　 B．1000，500　　　　　　　 C．1200，600　　　 D．800，400

2.导数的概念.

1.瞬时速度、瞬时变化率的概念.

3.例2中,计算第时和第时,原油温度的瞬时变化率,并说明它们的意义.

2.求曲线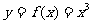在时的导数.

1.质点运动规律为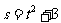,求质点在的瞬时速度为.

例1 (1)求函数在处的导数.

(2)求函数在附近的平均变化率,并求出该点处的导数.

分析: 先求,再求,最后求.

解: (1)法一 定义法(略)

　　 　　法二

(2)

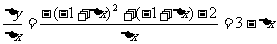
例2 将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,如果第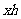时,原油的温度(单位: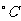)为,计算第时和第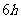时,原油温度的瞬时变化率,并说明它们的意义.

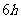解: 在第时和第时,原油温度的瞬时变化率就是和

根据导数定义

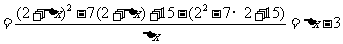
所以　 同理可得: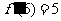

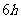在第时和第时,原油温度的瞬时变化率分别为和,

说明在第附近,原油温度大约以的速率下降

在第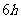附近,原油温度大约以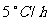的速率上升.

注: 一般地,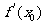反映了原油温度在时刻附近的变化情况.

2.导数的概念

从函数在处的瞬时变化率是:

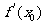我们称它为函数在出的导数,记作或

即

说明: (1)导数即为函数在处的瞬时变化率;

　　 　(2)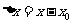,当时,,所以.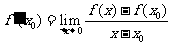

1.瞬时速度

我们把物体在某一时刻的速度称为瞬时速度.运动员的平均速度不能反映他在某一时刻的瞬时速度,那么,如何求运动员的瞬时速度呢？比如,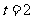时的瞬时速度是多少？考察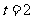附近的情况:

思考: 当趋近于时,平均速度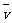有什么样的变化趋势？

结论: 当趋近于时,即无论从小于的一边,还是从大于的一边趋近于时,平均速度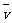都趋近于一个确定的值.

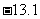从物理的角度看,时间间隔无限变小时,平均速度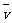就无限趋近于史的瞬时速度.因此,运动员在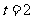时的瞬时速度是

为了表述方便,我们用

表示“当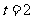,趋近于时,平均速度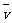趋近于定值”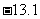

小结: 局部以匀速代替变速,以平均速度代替瞬时速度,然后通过取极限,从瞬时速度的近似值过渡到瞬时速度的精确值.

(二)探究

探究: 计算运动员在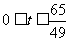这段时间里的平均速度,并思考以下问题:

(1)运动员在这段时间内使静止的吗？

(2)你认为用平均速度描述运动员的运动状态有什么问题吗？

探究过程: 如图是函数的图像,

结合图形可知,,

所以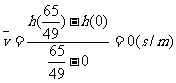

虽然运动员在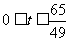这段时间里的平均速度为,

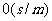但实际情况是运动员仍然运动,并非静止,

可以说明用平均速度不能精确描述运动员的运动状态.