
4.(2009安徽卷理)若集合 则A∩B是
则A∩B是 
(A)  (B)
(B)  (C)
(C)
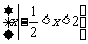 (D)
(D) 

5(2009江西卷理)已知全集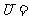
 中有m个元素,
中有m个元素,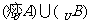 中有n个元素.若
中有n个元素.若 非空,则
非空,则 的元素个数为
的元素个数为
A.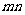 B.
B.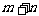 C.
C. D.
D.

3.(2009广东卷理)已知全集 ,集合
,集合 和
和 的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有
的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有


A. 3个 B. 2个 C. 1个 D. 无穷多个
2.(2009浙江理)设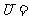
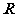 ,
,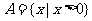 ,
,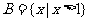 ,则
,则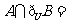 ( )
( ) 
A. B.
B.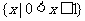 C.
C. D.
D.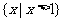

1.(2009全国卷Ⅰ理)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A B,则集合
B,则集合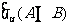 中的元素共有(A)
中的元素共有(A)
(A)3个 (B)4个 (C)5个 (D)6个 

1.(2009年上海卷理)已知集合 ,
, ,且
,且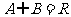 ,则实数a的取值范围是_____
,则实数a的取值范围是_____
考点2:考查集合运算
3. 利用反证法
例12 已知函数f(x)在区间(-∞,+∞)上是增函数,a,b∈R,若f(a)+f(b)≥f(-a)+f(-b).求证:a+b≥0.
证明 假设a+b<0,则a<-b,b<-a,
∵ 函数f(x)在区间(-∞,+∞)上是增函数,
∴ f(a) <f(-b),f(b) <f(-a),
∴ f(a)+f(b)<f(-a)+f(-b),这与已知矛盾,
∴ a+b<0不成立,即a+b≥0.
例13 设函数f(x)对定义域内任意实数都有f(x) ≠0,且f(x+y)=f(x)f(y)成立,求证:对定义域内任意x,都有f(x) >0.
 证明 假设在定义域内存在x0,使f(x0)≤ 0,
证明 假设在定义域内存在x0,使f(x0)≤ 0,
∵
∴ f(x0) >0,这与假设的f(x0)≤ 0矛盾,
所以假设不成立,故对定义域内任意x,都有f(x) >0.
以上我们利用抽象函数的特殊模型、函数性质、特殊方法等途径举例说明了求解抽象函数问题的一些策略.事实上处理这类问题时,常将几种解题策略综合使用,“多管齐下”方能游刃有余.
2. 利用递推法
例10 设函数f(x)的定义域为R,且对任意实数x,都有f(x)=f(x+1)-f(x+2),求证:f(x)是周期函数.
解 ∵ f(x)=f(x+1)-f(x+2),
∴ f(x+1)=f(x+2)-f(x+3),
将以上两式相加,得 f(x+3)=-f(x),
∴ f(x+6)=-f(x +3)=f(x),
∴ f(x)是周期函数,6是它的一个周期.
例11 f(x)是定义在正整数集的函数,且满足f(x+y)=f(x)+f(y)+xy
(x,y∈N+),f(1)=1,求函数f(x)的解析式.
解 令y=1,
∵ f(1)=1,
∴ f(x+1)=f(x)+f(1)+x, 即f(x+1)-f(x)=x+1,
则 f(2)-f(1)=2,
f(3)-f(2)=3,
……
f(x)-f(x-1)=x.
将以上各式相加,得 f(x)-f(1)=2+3+4+ …+x,
∴ f(x)=1+2+3+4+…+x=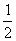 x(x+1) (x∈N+).
x(x+1) (x∈N+).
有些抽象函数问题,用常规方法来解决往往难于奏效,但用一些非常规方法来求解,常收到意想不到的效果.
1. 利用赋值法
例9 函数f(x)的定义域为R,对任意x、y∈R,都有f(x+y)+f(x-y)=
2f(x)f(y),且f(0)≠0.
(1)求证:f(0)=1;
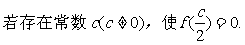 (2)求证:f(x)是偶函数;
(2)求证:f(x)是偶函数;
(3) ① 求证:对任意x∈R,有f(x+c)=
-f(x)成 立;② 求证:f(x)是周期函数.
解 (1)令x=y=0,则有2f(0)=2f2(0),
∵ f(0)≠0,
∴ f(0)=1.
(2)令x=0,则有f(y)+f(-y)= 2f(0)f(y),
∵ f(0)=1,
∴ f(-y)=f(y),
∴ f(x)是偶函数.
(3)① 分别用 (c≠0)替换x、y, 有f(x+c)+f(x)=2f(
(c≠0)替换x、y, 有f(x+c)+f(x)=2f( )f(
)f( ).
).
∵ f( )=0,
)=0,
∴ f(x+c)= -f(x) .
② 由①知 f(x+c)=-f(x),
用x+c替换x,有f(x+2c)=-f(x+c)=f(x),
∴ f(x)是以2c为周期的周期函数.
4. 利用对称性
例7 已知f(x)是奇函数,定义域为{x|x ∈R,x≠0},又f(x)在区间(0,+∞)上是增函数,且f(-1)=0,则满足f(x)>0的x的取值区间是 .
解 依已知条件作出f(x)的大致图象,如图1所示,从图象中可看出,当f(x)>0时,x的取值区间是(-1,0)∪(1,+∞).
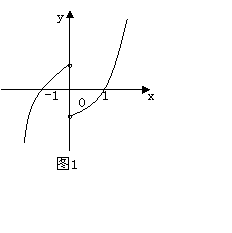
例8 定义在(-∞,+∞)上的函数y=f(x)在(-∞,2)上是增函数,且函数y=f(x+2)为偶函数,则f(-1),f(4),f(6)的大小关系为 .
解 设F(x)=f(x+2),
∵ F(x)为偶函数,
∴ F(-x)=F(x), 即f(2+x)=f(2-x),
∴ 函数f(x)的图象关于直线x=2对称,
∴ f(-1)=f(5),
∵ f(x)在(-∞,2)上是增函数,
∴ f(x)在(2,+∞)上是减函数,
∴ f(6)<f(5)<f(4), 即f(6)<f(-1)<f(4).
3. 利用周期性
例5 设函数f(x)在R上是奇函数,f(x+2)=-f(x) ,当0<x≤1时,f(x)=x,则f(7.5)= .
解 由f(x+2)=-f(x) ,得 f(x+4)=-f(x+2)=f(x),
则f(x)是以4为周期的周期函数,且是奇函数,
于是 f(7.5)=f(2×4-0.5)=f(-0.5)=-f(0.5)=-0.5.
 例6 已知函数f(x)满足f(1)=2,f(x+1)=
例6 已知函数f(x)满足f(1)=2,f(x+1)=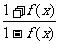 ,则 f(2007)= .
,则 f(2007)= .
解 ∵
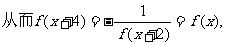

∴ f(x)是以4为周期的周期函数,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com