
后记:
对数运算性质及推导;运用对数运算性质;换底公式.
5. 设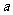 、
、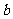 、
、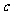 为正数,且
为正数,且 ,求证:
,求证: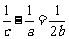
4. 试求 的值
的值
3、计算: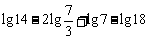 ;
;  ;
; 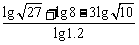 .
.
2.
设 ,
, ,试用
,试用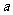 、
、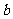 表示
表示 .
.
变式:已知lg2=0.3010,lg3=0.4771,求lg6、lg12、lg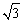 的值.
的值.
1、P681、2、3
1. 教学例题:
例1. 判断下列式子是否正确,(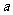 >0且
>0且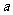 ≠1,
≠1, >0且
>0且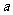 ≠1,
≠1, >0,
>0, >
> ),
),
(1)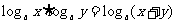 (2)
(2)
(3)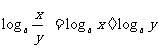 (4)
(4)
(5) (6)
(6)
(7)
例2( P65例3例4):用 ,
, ,
,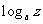 表示出(1)(2)小题,并求出(3)、(4)小题的值.
表示出(1)(2)小题,并求出(3)、(4)小题的值.
(1) (2)
(2) (3)
(3)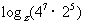 (4)
(4)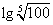
1. 教学对数运算性质及推导:
① 引例: 由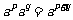 ,如何探讨
,如何探讨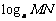 和
和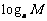 、
、
 之间的关系?
之间的关系?
设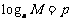 ,
, 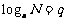 ,由对数的定义可得:M=
,由对数的定义可得:M= ,N=
,N=

∴MN=
 =
=
∴ MN=p+q,即得
MN=p+q,即得 MN=
MN= M +
M +  N
N
② 探讨:根据上面的证明,能否得出以下式子?
如果 a > 0,a ¹ 1,M > 0, N > 0 ,则
 ;
; 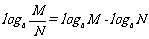 ;
; 
①
讨论:自然语言如何叙述三条性质? 性质的证明思路?(运用转化思想,先通过假设,将对数式化成指数式,并利用幂运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式 )
)
④ 运用换底公式推导下列结论: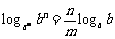 ;
;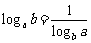
2. 提问:指数幂的运算性质?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com