8.(2009届山东威海一中高三月考1)如图所示，两光滑斜面的倾角分别为30°和45°，质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦)，分别置于两个斜面上并由静止释放；若交换两滑块位置，再由静止释放．则在上述两种情形中正确的有(.BC　　　 )

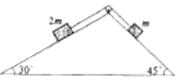
A.质量为2m的滑块受到重力、绳的张力、沿斜面的下滑力和斜面的支持力的作用

B.质量为m的滑块均沿斜面向上运动

C. 系统在运动中机械能均守恒

D.绳对质量为m滑块的拉力均大于该滑块对绳的拉力

7.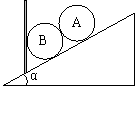(2009上海崇明县高三期末)如图所示，两个完全相同的光滑球的质量为m，放在竖直挡板和倾角为α的固定斜面间。若缓慢转动挡板至斜面垂直，则在此过程中　　　 (　 AB　 )

A.A、B两球间的弹力不变；　

B.B球对挡板的压力逐渐减小；

C.B球对斜面的压力逐渐增大；　 　

D.A球对斜面的压力逐渐增大。

6.(2009年广大附中)在粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m₁和m₂的木块,m₁>m₂，如图3所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块(D )

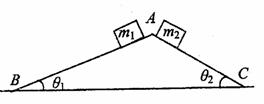
A．有摩擦力的作用,摩擦力的方向水平向右

B．有摩擦力的作用,摩擦力的方向水平向左

C．有摩擦力的作用,但摩擦力的方向不能确定,因 为m₁、m₂、θ₁、θ₂的数值并未给出

D．以上结论都不对

5.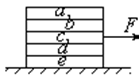(2009　届江苏苏州中学高三月考) 五本书相叠放在水平桌面上，用水平力F拉中间的书C但未拉动，各书仍静止(如图)。关于它们所受摩擦力的情况，以下判断中正确的是　 (　 ABD　 )

A．书e受两个摩擦力作用 　　B．书b受到一个摩擦力作用

C．书c受到一个摩擦力作用　 D．书a不受摩擦力作用

4.(广东中山龙山中学09届高三第二次月考)用轻弹簧竖直悬挂质量为m的物体，静止时弹簧伸长量为L 。现用该弹簧沿斜面方向拉住质量为2 m的物体，系统静止时弹簧伸长量也为L 。斜面倾角为30°，如图所示。则物体所受摩擦力(A)

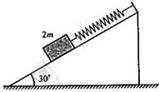A．等干零

B．大小为mg，方向沿斜面向下

C．大小为mg，方向沿斜面向上

D． 大小为mg，方向沿斜面向上

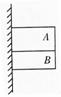
3.(2009年广东潮州市高三下学期模拟)如图A、B两物体叠放在一起，用手托住，让它们静靠在竖直墙边，然后释放，它们同时沿墙面向下滑，已知m_A＞m_B,则物体B　　 　(.A )

A．只受一个重力

B．受到重力和一个摩擦力

C．受到重力、一个弹力和一个摩擦力

D．受到重力、一个摩擦力和两个弹力

2.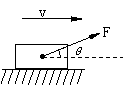2009上海南汇区高三期末)如图所示，质量为m的物体放在水平桌面上，在与水平方向成θ角的拉力F作用下加速向前运动，已知物体与桌面间的动摩擦因数为μ，则下列判断正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ( B )

A．物体受到的摩擦力为F·cosθ

B．物体受到的摩擦力为μmg

C．物体对地面的压力为mg

D．物体受到地面的的支持力为mg－F·sinθ

1.(安徽凤阳荣达学校2009届高三物理第三次月考)如图所示，物体A、B、C叠放在水平桌面上，水平力F作用于C物体，使A、B、C以共同速度向右匀速运动，那么关于物体

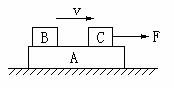受几个力的说法正确的是　　　 (　 A　 )

A．A 受6个，B受2个，C受4个　 　 　

B．A 受5个，B受3个，C受3个　　　

C．A 受5个，B受2个，C受4个　　　　 　

D．A 受6个，B受3个，C受4个　

2009年力、物体的平衡

6．平衡条件的应用技巧

形如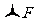=0的平衡条件从本质上看应该是处于平衡状态下的物体所受到的各个外力之间的某种矢量关系，准确把握平衡条件所表现出的矢量关系，就能在平衡条件的应用中充分展现其应用的技巧。

(1)正交分解法：这是平衡条件的最基本的应用方法。其实质就是将各外力间的矢量关系转化为沿两个坐标轴方向上的力分量间的关系，从而变复杂的几何运算为相对简单的代数运算。即

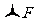=0→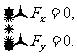

　 作为基本的应用方法，正交分解法的应用步骤为：

　　 ①确定研究对象；

②分析受力情况；

③建立适当坐标；

④列出平衡方程.

(2)多边形(三角形)法。

如果物体受到n个共面的力而处于平衡状态，则表示　 　　　　　　　　　　

这n个力的n条有向线段可以依次首尾相接而构成一个封闭的“力的n边形”，特别是当n=3时，则将构成一个封闭的“力的三角形”。

(3)相似形法。

如果物体受到共面的力的作用而处于平衡状态，一方面表示这些力的有向线段将构成封闭的“力的多边形”，另一方面若存在着与之相似的“几何多边形”，则可以利用相似多边形的“对应边成比例”的特性来表现平衡条件中的各个力之间的关系。

　(6)共点法。

　 物体受到共面的力的作用而处地平衡状态，若表示这些力的有向线段彼此间不平行，则它们必将共点。