
例1已知



例2已知f(x)=x2-1 g(x)=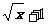 求f[g(x)]
求f[g(x)]
解:f[g(x)]=(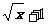 )2-1=x+2
)2-1=x+2
例3 求下列函数的定义域:
① ②
②
③
 ④
④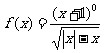
⑤
解:①要使函数有意义,必须: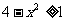 即:
即: 
∴函数 的定义域为: [
的定义域为: [ ]
]
②要使函数有意义,必须:

∴定义域为:{ x| }
}
③要使函数有意义,必须:  Þ
Þ 
∴函数的定义域为:
④要使函数有意义,必须: 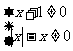

∴定义域为:
⑤要使函数有意义,必须: 

即 x< 或 x>
或 x> ∴定义域为:
∴定义域为:
例4 若函数 的定义域是R,求实数a 的取值范围
的定义域是R,求实数a 的取值范围
解:∵定义域是R,∴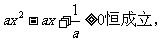
∴
例5 若函数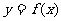 的定义域为[-1,1],求函数
的定义域为[-1,1],求函数
 的定义域
的定义域
解:要使函数有意义,必须:

∴函数
 的定义域为:
的定义域为: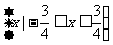
求用解析式y=f(x)表示的函数的定义域时,常有以下几种情况:
①若f(x)是整式,则函数的定义域是实数集R;
②若f(x)是分式,则函数的定义域是使分母不等于0的实数集;
③若f(x)是二次根式,则函数的定义域是使根号内的式子大于或等于0的实数集合;
④若f(x)是由几个部分的数学式子构成的,则函数的定义域是使各部分式子都有意义的实数集合;
⑤若f(x)是由实际问题抽象出来的函数,则函数的定义域应符合实际问题.
例6 已知f(x)满足 ,求
,求 ;
;
∵已知 ①,
①,
将①中x换成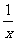 得
得 ②,
②,
①×2-②得 ∴
∴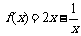 .
.
例7 设二次函数 满足
满足 且
且 =0的两实根平方和为10,图象过点(0,3),求
=0的两实根平方和为10,图象过点(0,3),求 的解析式.
的解析式.
解:设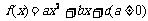 ,
,
∵图象过点(0,3),∴有f(0)=c=3,故c=3;
又∵f(x)满足 且
且 =0的两实根平方和为10,
=0的两实根平方和为10,
∴得对称轴x=2且 =10,
=10,
即 且
且 ,∴a=1,b=-4,∴
,∴a=1,b=-4,∴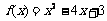
4.复合函数:设 f(x)=2x-3,g(x)=x2+2,则称 f[g(x)] =2(x2+2)-3=2x2+1(或g[f(x)] =(2x-3)2+2=4x2-12x+11)为复合函数
3.分段函数:有些函数在它的定义域中,对于自变量x的不同取值范围,对应法则不同,这样的函数通常称为分段函数.分段函数是一个函数,而不是几个函数.
2.求函数定义域的基本方法
我们知道,根据函数的定义,所谓“给定一个函数”,就应该指明这个函数的定义域和对应法则(此时值域也往往随着确定),不指明这两点是不能算给定了一个函数的,那么为什么又在给定函数之后来求它的定义域呢?这是由于用解析式表示函数时,我们约定:如果不单独指出函数的定义域是什么集合,那么函数的定义域就是能使这个式子有意义的所有实数x的集合.有这个约定,我们在用解析式给出函数的对应法则的同时也就给定了定义域,而求函数的定义域就是在这个意义之下写出使式子有意义的所有实数组成的集合.
1.区间的概念和记号
在研究函数时,常常用到区间的概念,它是数学中常用的述语和符号.
设a,b R ,且a<b.我们规定:
R ,且a<b.我们规定:
①满足不等式a x
x b的实数x的集合叫做闭区间,表示为[a,b];
b的实数x的集合叫做闭区间,表示为[a,b];
②满足不等式a<x<b的实数x的集合叫做开区间,表示为(a,b);
③满足不等式a x<b 或a<x
x<b 或a<x b的实数x的集合叫做半开半闭区间,分别表示为[a,b) ,(a,b].
b的实数x的集合叫做半开半闭区间,分别表示为[a,b) ,(a,b].
这里的实数a和b叫做相应区间的端点.
在数轴上,这些区间都可以用一条以a和b为端点的线段来表示,在图中,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点:
|
定 义 |
名 称 |
符 号 |
数 轴 表 示 |
{x|a x x b} b} |
闭区间 |
[a,b] |
 |
|
{x|a<x<b} |
开区间 |
(a,b) |
 |
{x|a x<b} x<b} |
左闭右开区间 |
[a,b] |
 |
{x|a<x b} b} |
左开右闭区间 |
(a,b) |
 |
这样实数集R也可用区间表示为(- ,+
,+ ),“
),“ ”读作“无穷大”,“-
”读作“无穷大”,“- ”读作“负无穷大”,“+
”读作“负无穷大”,“+ ”读作“正无穷大”.还可把满足x
”读作“正无穷大”.还可把满足x a,x>a,x
a,x>a,x b,x<b的实数x的集合分别表示为[a,+
b,x<b的实数x的集合分别表示为[a,+
 ,(a,+
,(a,+ ),(-
),(-  ,b
,b ,(-
,(-  ,b).
,b).
注意:书写区间记号时:
①有完整的区间外围记号(上述四者之一);
②有两个区间端点,且左端点小于右端点;
③两个端点之间用“,”隔开.
函数的三要素是:定义域、值域和定义域到值域的对应法则;对应法则是函数的核心(它规定了x和y之间的某种关系),定义域是函数的重要组成部分(对应法则相同而定义域不同的映射就是两个不同的函数);定义域和对应法则一经确定,值域就随之确定
前面我们已经学习了函数的概念,,今天我们来学习区间的概念和记号
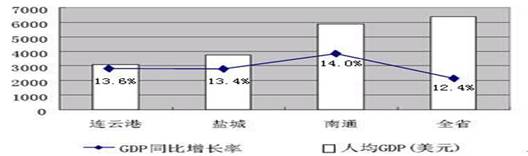
27.(18分)材料一:2009年江苏省及沿海三市GDP统计
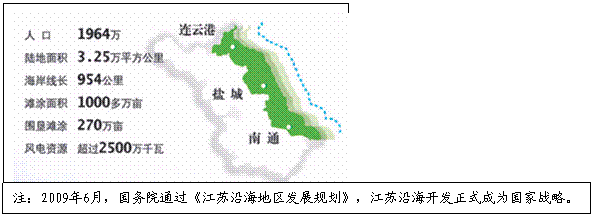
材料二:江苏沿海三市资源情况

(1)指出表一反映的经济信息。(6分)
(2)在不少人眼中,江苏沿海地区是个“经济洼地”,但在专家眼里却是一块不可多得的开发潜力巨大的“风水宝地”。请结合材料,从《经济生活》角度,说明如何才能将“经济洼地”变成“风水宝地”。(12分)
26.2010年3月25日,欧盟春季首脑会议在布鲁塞尔开幕。欧盟27国领导人重点讨论了欧
盟未来10年经济发展战略和应对全球气候变化两大议题。这体现了欧盟
①是一体化程度最高的国际组织 ②以实现社会经济可持续发展为宗旨
③在国际事务中能发挥重大作用 ④以磋商代替谈判的全新的合作方式
A.①② B.①④ C.②③ D.③④
25.对美国经济发展和就业的问题,奥巴马认为是共和党执政时期“放手不管”的治理理念
把美国带入衰退;共和党认为是奥巴马政府提高税赋、监管繁苛,扰乱了企业雇主的规划。
此类差别及其相应的政策
A.成为两党制运行的基础 B.反映了两党的本质区别
C.体现了一定程度的民意 D.确保了两党的轮流执政
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com