
3、注意解三角形中的应用题,应用题是数学的一个难点,平时应加强训练。
2、注意知识之间的横向联系,三角函数知识之间的联系,三角函数与其它知识的联系,如三角函数与向量等。
1、本节公式较多,但都是有规律的,认真总结规律,记住公式是解答三角函数的关键。
5.高考考点分析
近几年高考中,三角函数主要以选择题和解答题的形式出现。主要考察内容按综合难度分,我认为有以下几个层次:
第一层次:通过诱导公式和倍角公式的简单运用,解决有关三角函数基本性质的问题。如判断符号、求值、求周期、判断奇偶性等。
第二层次:三角函数公式变形中的某些常用技巧的运用。如辅助角公式、平方公式逆用、切弦互化等。
第三层次:充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质,解决较复杂的函数问题。如分段函数值,求复合函数值域等。
4.解答三角高考题的策略。
(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化。
3.证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等。
2.证明三角等式的思路和方法。
(1)思路:利用三角公式进行化名,化角,改变运算结构,使等式两边化为同一形式。
(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法。
1.三角函数恒等变形的基本策略。
(1)注意隐含条件的应用:1=cos2x+sin2x。
(2)角的配凑。α=(α+β)-β,β= -
- 等。
等。
(3)升幂与降幂。主要用2倍角的余弦。
(4)化弦(切)法,用正弦定理或余弦定理。
(5)引入辅助角。asinθ+bcosθ= sin(θ+
sin(θ+ ),这里辅助角
),这里辅助角 所在象限由a、b的符号确定,
所在象限由a、b的符号确定, 角的值由tan
角的值由tan =
= 确定。
确定。
考点一:三角函数的概念
[内容解读]三角函数的概念包括任意角的概念和弧度制,任意三角函数(正弦、余弦、正切)的定义,能进行弧度与角度的互化,会由角的终边所经过点的坐标求该角的三角函数值。在学习中要正确区分象限角及它们的表示方法,终边相同角的表示方法,由三角函数的定义,确定终边在各个象限的三角函数的符号。在弧度制下,计算扇形的面积和弧长比在角度制下计算更为方便、简洁。
[命题规律]在高考中,主要考查象限角,终边相同的角,三角函数的定义,一般以选择题和填空题为主。
例1、(2008北京文)若角α的终边经过点P(1,-2),则tan 2α的值为 .
解: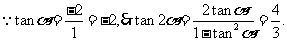
点评:一个角的终边经过某一点,在平面直角坐标系中画出图形,用三角函数的定义来求解,或者不画图形直接套用公式求解都可以。
考点二:同角三角函数的关系
[内容解读]同角三角函数的关系有平方关系和商数关系,用同角三角函数定义反复证明强化记忆,在解题时要注意 ,这是一个隐含条件,在解题时要经常能想到它。利用同角的三角函数关系求解时,注意角所在象限,看是否需要分类讨论。
,这是一个隐含条件,在解题时要经常能想到它。利用同角的三角函数关系求解时,注意角所在象限,看是否需要分类讨论。
[命题规律]在高考中,同角的三角函数的关系,一般以选择题和填空题为主,结合坐标系分类讨论是关键。
例2、(2008浙江理)若 则
则 =( )
=( )
(A)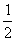 (B)2
(C)
(B)2
(C) (D)
(D)
解:由 可得:由
可得:由 ,
,
又由 ,可得:
,可得: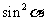 +(
+( )2=1
)2=1
可得 =-
=-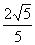 ,
, =-
=- ,
,
所以, =
= =2。
=2。
点评:对于给出正弦与余弦的关系式的试题,要能想到隐含条件: ,与它联系成方程组,解方程组来求解。
,与它联系成方程组,解方程组来求解。
例3、(2007全国卷1理1) 是第四象限角,
是第四象限角, ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
解:由 ,所以,有
,所以,有 ,
, 是第四象限角,
是第四象限角,
解得:

点评:由正切值求正弦值或余弦值,用到同角三角函数公式: ,同样要能想到隐含条件:
,同样要能想到隐含条件: 。
。
考点三: 诱导公式
[内容解读]诱导公式用角度和弧度制表示都成立,记忆方法可以概括为“奇变偶不变,符号看象限”,“变”与“不变”是相对于对偶关系的函数而言的,sinα与cosα对偶,“奇”、“偶”是对诱导公式中 +α的整数k来讲的,象限指
+α的整数k来讲的,象限指 +α中,将α看作锐角时,
+α中,将α看作锐角时, +α所在象限,如将cos(
+α所在象限,如将cos( +α)写成cos(
+α)写成cos(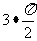 +α),因为3是奇数,则“cos”变为对偶函数符号“sin”,又
+α),因为3是奇数,则“cos”变为对偶函数符号“sin”,又 +α看作第四象限角,cos(
+α看作第四象限角,cos( +α)为“+”,所以有cos(
+α)为“+”,所以有cos( +α)=sinα。
+α)=sinα。
[命题规律]诱导公式的考查,一般是填空题或选择题,有时会计算特殊角的三角函数值,也有些大题用到诱导公式。
例4、(2008陕西文)  等于( )
等于( )
A. B.
B.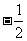 C.
C.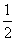 D.
D.
解: =
=
点评:本题是对诱导公式和特殊角三角函数值的考查,熟练掌握诱导公式即可。
答案:
例5、(2008浙江文)若 .
.
解:由 可知,
可知, ;而
;而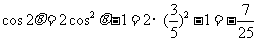 。
。
点评:本小题主要考查诱导公式及二倍角公式的应用,难度不算大,属基础题,熟练掌握公式就能求解。
考点四:三角函数的图象和性质
[内容解读]理解正、余弦函数在]0,2π],正切函数在(- ,
, )的性质,如单调性、最大值与最小值、周期性,图象与x轴的交点,会用五点法画函数
)的性质,如单调性、最大值与最小值、周期性,图象与x轴的交点,会用五点法画函数 的图象,并理解它的性质:
的图象,并理解它的性质:
(1)函数图象在其对称轴处取得最大值或最小值,且相邻的最大值与最小值间的距离为其函数的半个周期;
(2)函数图象与x轴的交点是其对称中心,相邻两对称中心间的距离也是其函数的半个周期;
(3)函数取最值的点与相邻的与x轴的交点间的距离为其函数的 个周期。
个周期。
注意函数图象平移的规律,是先平移再伸缩,还是先伸缩再平移。
[命题规律]主要考查三角函数的周期性、单调性、有界性、图象的平移等 ,以选择题、解答题为主,难度以容易题、中档题为主。
例6、(2008天津文)设 ,
, ,
,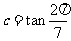 ,则( )
,则( )
A. B.
B. C.
C.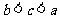 D.
D.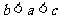
解: ,因为
,因为 ,所以
,所以 ,选D.
,选D.
点评:掌握正弦函数与余弦函数在[0, ],[
],[ ,
,  ]的大小的比较,画出它们的图象,从图象上能比较它们的大小,另外正余弦函数的值域:[0,1],也要掌握。
]的大小的比较,画出它们的图象,从图象上能比较它们的大小,另外正余弦函数的值域:[0,1],也要掌握。
例7、(2008山东文、理)函数 的图象是( )
的图象是( )
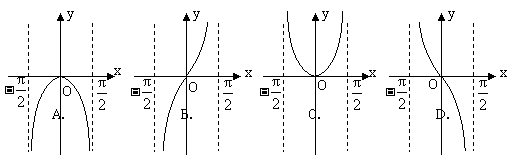

解:  是偶函数,可排除B、D,由
是偶函数,可排除B、D,由 的值域可以确定.因此本题应选A.
的值域可以确定.因此本题应选A.
点评:本小题主要考查复合函数的图像识别,充分掌握偶函数的性质,余弦函数的图象及性质,另外,排除法,在复习时应引起重视,解选择题时,经常采用排除法。
例8、(2008天津文)把函数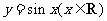 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动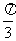 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的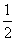 倍(纵坐标不变),得到的图象所表示的函数是( )
倍(纵坐标不变),得到的图象所表示的函数是( )
A. B.
B.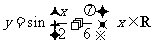
C. D.
D.
解:
y=



 ,故选(C)。
,故选(C)。
点评:三角函数图象的平移、伸缩变换是高考的热门试题之一,牢固变换的方法,按照变换的步骤来求解即可。
例9、(2008浙江理)在同一平面直角坐标系中,函数 的图象和直线
的图象和直线 的交点个数是( )
的交点个数是( )
(A)0 (B)1 (C)2 (D)4
解:原函数可化为:
 =
=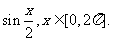 作出原函数图像,
作出原函数图像,
截取 部分,其与直线
部分,其与直线 的交点个数是2个.
的交点个数是2个.
点评:本小题主要考查三角函数图像的性质问题,学会五点法画图,取特殊角的三角函数值画图。
考点五:三角恒等变换
[内容解读]经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用;;能从两角差的余弦公式,导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系,公式之间的规律,能用上述的公式进行简单的恒等变换;注意三角恒等变换与其它知识的联系,如函数的周期性,三角函数与向量等内容。
[命题规律]主要考查三角函数的化简、求值、恒等变换。题型主、客观题均有,近几年常有一道解答题,难度不大,属中档题。
例10、(2008惠州三模)已知函数
(I)求函数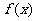 的最小正周期; (II)求函数
的最小正周期; (II)求函数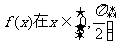 的值域.
的值域.
解:


 (I)
(I)
(II)∴ ∴
∴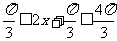 ∴
∴ 
所以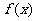 的值域为:
的值域为:
点评:本题考查三角恒等变换,三角函数图象的性质,注意掌握在给定范围内,三角函数值域的求法。
例11、(2008广东六校联考)已知向量 =(cos
=(cos x,sin
x,sin x),
x),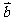 =(
=( ),且x∈[0,
),且x∈[0, ].
].
(1)求
(2)设函数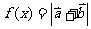 +
+ ,求函数
,求函数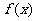 的最值及相应的
的最值及相应的 的值。
的值。
解:(I)由已知条件:  , 得:
, 得: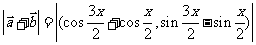

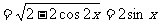
(2)

 ,因为:
,因为: ,所以:
,所以:
所以,只有当: 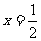 时,
时,  ,
, ,或
,或 时,
时,
点评:本题是三角函数与向量结合的综合题,考查向量的知识,三角恒等变换、函数图象等知识。
例12、(2008北京文、理)已知函数 的最小正周期为π.
的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在区间[0, ]上的取值范围.
]上的取值范围.
解:(Ⅰ)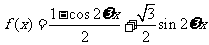
=
=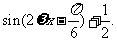
因为函数f(x)的最小正周期为π,且ω>0,所以
解得ω=1.
(Ⅱ)由(Ⅰ)得
因为0≤x≤ ,
,
所以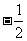 ≤
≤ ≤
≤
所以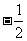 ≤
≤ ≤1.
≤1.
因此0≤ ≤
≤ ,即f(x)的取值范围为[0,
,即f(x)的取值范围为[0, ]
]
点评:熟练掌握三角函数的降幂,由2倍角的余弦公式的三种形式可实现降幂或升幂,在训练时,要注意公式的推导过程。
考点六:解三角形
[内容解读]掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题,能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题。
解三角形时,要灵活运用已知条件,根据正、余弦定理,列出方程,进而求解,最后还要检验是否符合题意。
[命题规律]本节是高考必考内容,重点为正余弦定理及三角形面积公式,考题灵活多样,近几年经常以解答题的形式来考查,若以解决实际问题为背景的试题,有一定的难度。
例13、(2008广东五校联考)在⊿ABC中,角A、B、C所对的边分别为a、b、c,且
(1)求tanC的值; (2)若⊿ABC最长的边为1,求b。
解:(1)
 B锐角,
B锐角,
且 ,
, ,
,
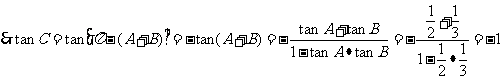
(2)由(1)知C为钝角, C是最大角,最大边为c=1,
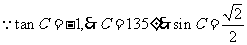 ,
,
由正弦定理: 得
得 。
。
点评:本题考查同角三角函数公式,两角和的正切,正弦定理等内容,综合考查了三角函数的知识。在做练习,训练时要注意加强知识间的联系。
例14、(2008海南、宁夏文)如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2。(1)求cos∠CBE的值;(2)求AE。
解:(Ⅰ)因为 ,
, ,
,
所以 .
.
 所以
所以 .
.
(Ⅱ)在 中,
中, ,
,
由正弦定理 .
.
故


点评:注意用三角恒等变换公式,由特殊角45度,30度,60度,推导15度,75度的三角函数值,在用正弦定理时,注意角与它所对边的关系。
例15、(2008湖南理)在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东 且与点A相距40
且与点A相距40 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东 +
+ (其中sin
(其中sin =
= ,
, )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
解: (I)如图,AB=40 ,AC=10
,AC=10 ,
,


由于 ,所以cos
,所以cos =
=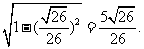
由余弦定理得BC=
所以船的行驶速度为 (海里/小时).
(海里/小时).
(II) 如图所示,以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),
BC与x轴的交点为D.
由题设有,x1=y1=  AB=40,
AB=40,
x2=ACcos ,
,
y2=ACsin
所以过点B、C的直线l的斜率k= ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=
所以船会进入警戒水域.
点评:三角函数在实际问题中有很多的应用,随着课改的深入,联系实际,注重数学在实际问题的应用将分是一个热点。
(三)正弦型函数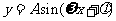 的图象变换方法如下:
的图象变换方法如下:
先平移后伸缩
 的图象
的图象
得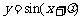 的图象
的图象
得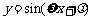 的图象
的图象
得 的图象
的图象
得 的图象.
的图象.
先伸缩后平移
 的图象
的图象
得 的图象
的图象
得 的图象
的图象
得 的图象
的图象 得
得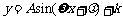 的图象.
的图象.
5、解三角形
Ⅰ.正、余弦定理⑴正弦定理 (
( 是
是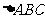 外接圆直径)
外接圆直径)
注:① ;②
;② ;③
;③ 。
。
⑵余弦定理: 等三个;注:
等三个;注: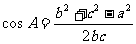 等三个。
等三个。
Ⅱ。几个公式:
⑴三角形面积公式: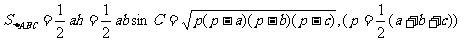 ;
;
⑵内切圆半径r= ;外接圆直径2R=
;外接圆直径2R=
⑶在使用正弦定理时判断一解或二解的方法:⊿ABC中,
Ⅲ.已知 时三角形解的个数的判定:
时三角形解的个数的判定:
其中h=bsinA,
⑴A为锐角时:
 ①a<h时,无解;
①a<h时,无解;
②a=h时,一解(直角);③h<a<b时,两解(一锐角,一钝角);④a b时,一解(一锐角)。
b时,一解(一锐角)。
⑵A为直角或钝角时:①a b时,无解;②a>b时,一解(锐角)。
b时,无解;②a>b时,一解(锐角)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com