
4.平行向量:①方向相同或相反的非零向量叫平行向量;②我们规定 与任一向量平行.向量
与任一向量平行.向量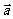 、
、 、
、 平行,记作
平行,记作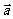 ∥
∥ ∥
∥ .共线向量与平行向量关系:平行向量就是共线向量.
.共线向量与平行向量关系:平行向量就是共线向量.
3.零向量、单位向量:①长度为0的向量叫零向量,记为 ; ②长度为1个单位长度的向量,叫单位向量.(注:
; ②长度为1个单位长度的向量,叫单位向量.(注: 就是单位向量)
就是单位向量)
2.向量的表示方法:①用有向线段表示;②用字母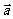 、
、 等表示;③平面向量的坐标表示:分别取与
等表示;③平面向量的坐标表示:分别取与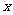 轴、
轴、 轴方向相同的两个单位向量
轴方向相同的两个单位向量 、
、 作为基底。任作一个向量
作为基底。任作一个向量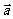 ,由平面向量基本定理知,有且只有一对实数
,由平面向量基本定理知,有且只有一对实数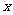 、
、 ,使得
,使得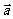
 ,
, 叫做向量
叫做向量 的(直角)坐标,记作
的(直角)坐标,记作 ,其中
,其中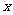 叫做
叫做 在
在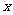 轴上的坐标,
轴上的坐标, 叫做
叫做 在
在 轴上的坐标, 特别地,
轴上的坐标, 特别地,
 ,
,
 ,
,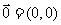 。
。 ;若
;若 ,
, ,则
,则 ,
,
1.向量的概念:既有大小又有方向的量叫向量,有二个要素:大小、方向.
5.利用函数知识解应用题是高考重点,应引起重视.
4.含参数函数的讨论是函数问题中的难点及重点,复习时应适当加强这方面的训练,做到条理清楚、分类明确、不重不漏.
3.二次函数是初中、高中的结合点,应引起重视,复习时要适当加深加宽.二次函数与二次方程、二次不等式有着密切的联系,要沟通这些知识之间的内在联系,灵活运用它们去解决有关问题.
2.掌握函数图象的基本变换,如平移、翻转、对称等.
基本函数:一次函数、二次函数、指数函数与对数函数,它们的图象与性质是函数的基石,判断、证明与应用函数的三大特性(单调性、奇偶性、周期性)是高考命题的切入点,有单一考查,也有综合考查.函数的图象、图象的变换是高考热点,应用函数知识解其他问题,特别是解应用题能很好地考查学生分析问题、解决问题的能力,这类问题在高考中具有较强的生存力.配方法、待定系数法、数形结合法、分类讨论等,这些方法构成了函数这一章应用的广泛性、解法的多样性和思维的创造性,这均符合高考试题改革的发展趋势.
特别在“函数”这一章中,数形结合的思想比比皆是,深刻理解和灵活运用这一思想方法,不仅会给解题带来方便,而且这正是充分把握住了中学数学的精髓和灵魂的体现.
复习函数时要注意:
1.深刻理解一些基本函数,如二次函数、指数函数、对数函数的图象与性质,对数与形的基本关系能相互转化.
(二)2009年高考预测
1.考查有关函数单调性和奇偶性的试题,从试题上看,抽象函数和具体函数都有,有向抽象函数发展的趋势,另外试题注重对转化思想的考查,且都综合地考查单调性与奇偶性.
2.考查与函数图象有关的试题,要从图中(或列表中)读取各种信息,注意利用平移变换、伸缩变换、对称变换,注意函数的对称性、函数值的变化趋势,培养运用数形结合思想来解题的能力.
3.考查与指数函数和对数函数有关的试题.对指数函数与对数函数的考查,大多以基本函数的性质为依托,结合运算推理来解决.
4加强函数思想、转化思想的考查是高考的一个重点.善于转化命题,引进变量建立函数,运用变化的方法、观点解决数学试题以提高数学意识,发展能力.
5、注意与导数结合考查函数的性质.
6、函数的应用,是与实际生活结合的试题,应加强重视。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com