
4. (2005江西)已知实数a、b满足等式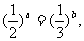 下列五个关系式:
下列五个关系式:
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
[填空题]
3.(2005天津)已知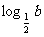 <
<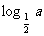 <
< 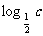 ,则 ( )
,则 ( )
A.2b>2a>2c B.2a>2b>2c C.2c>2b>2a D.2c>2a>2b
2.已知a>b>c>0,若P= ,Q=
,Q=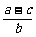 ,则 ( )
,则 ( )
A.P≥Q B.P≤Q C.P>Q D.P<Q
1. 若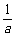 <
<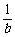 <0,则下列结论不正确的是 ( )
<0,则下列结论不正确的是 ( )
A.a2<b2 B.ab<b2
C.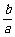 +
+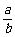 >2 D.|a|+|b|>|a+b|
>2 D.|a|+|b|>|a+b|
2.总结所学不等式证明的方法:
同步练习 6.4不等式的证明II
[选择题]
1.高考中一般不出现单一的不等式的证明题,常常与函数、数列、三角、方程综合在一起,所以,除掌握常用的三种方法外,还需了解其他方法,如函数的单调性法、判别式法、换元法(特别是三角换元)、放缩法以及数学归纳法等.
[例1]已知a,b∈R,且a+b=1
求证: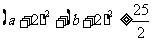
证法一:比较法,作差消b,化为a的二次函数。
也可用分析法、综合法,反证法,实质与比较法相同。
证法二:(放缩法)∵
∴左边=
 =右边
=右边
证法三:(均值换元法)∵ ,
,
所以可设 ,
, ,
,
∴左边=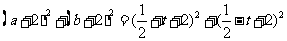
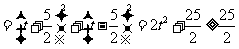 =右边
=右边
当且仅当t=0时,等号成立
点评:形如a+b=1结构式的条件,一般可以采用均值换元
证法四:(判别式法)
设y=(a+2)2+(b+2)2,
由a+b=1,有 ,
,
所以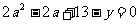 ,
,
因为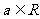 ,所以
,所以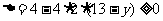 ,即
,即
故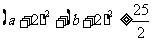
◆温馨提示:注意体验不等式证明方法的灵活性和各种证明方法间的内在联系.
[例2](1)设 ,且
,且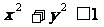 ,求证:
,求证: ;
;
(2)设 ,且
,且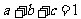 ,求证:
,求证:
[证明] (1)设
则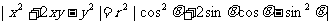 ,
,
= 。
。
(2)设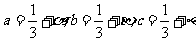 ,
,
∵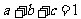 ,∴
,∴ 。
。
于是 。
。
[例3]已知a>1,n≥2,n∈N*.
求证: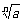 -1<
-1< .
.
证法一:要证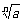 -1<
-1< ,
,
即证a<( +1)n.
+1)n.
令a-1=t>0,则a=t+1.
也就是证t+1<(1+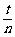 )n.
)n.
∵(1+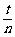 )n=1+C
)n=1+C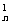
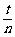 +…+C
+…+C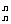 (
(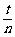 )n>1+t,
)n>1+t,
即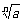 -1<
-1< 成立.
成立.
证法二:设a=xn,x>1.
于是只要证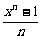 >x-1,
>x-1,
即证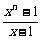 >n.联想到等比数列前n项和
>n.联想到等比数列前n项和
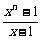 =1+x+…+xn-1>n.
=1+x+…+xn-1>n.
∴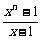 >n.
>n.
[例4]已知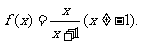
(1)求f(x)的单调区间;
(2)求证:x>y>0,有f(x+y)<f(x)+f(y);
(3)若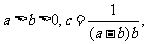 求证:
求证: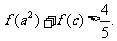
解: (1) 对 已 知 函 数 进 行 降 次 分 项 变 形 , 得 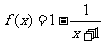 ,
,
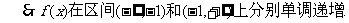
(2)∵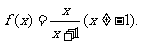
∴
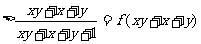
而 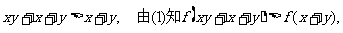

另法: 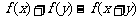
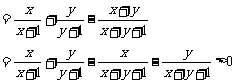
⑶ 
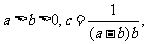
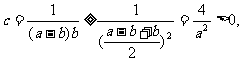
∴

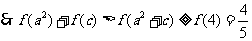
点评:函 数 与
不 等 式 证 明 的 综 合 题 在 高 考 中 常 考 常 新 , 是 既 考 知 识 又 考 能 力 的
好 题 型 , 在 高 考 备 考 中 有 较 高 的 训 练 价 值 .
.
[研讨.欣赏]数列{an}满足a1=1且an+1=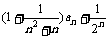 (n≥1)
(n≥1)
(1)用数学归纳法证明:an≥2(n≥2);
(2)已知不等式ln(1+x)<x对x>0成立,证明:an<e2(n≥1),其中无理数e=2.71828….
证明:(1)①当n=2时,a2=2≥2,不等式成立.
②假设当n=k(k≥2)时不等式成立,即ak≥2(k≥2),
那么ak+1=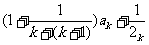 ≥2.这就是说,当n=k+1时不等式成立.
≥2.这就是说,当n=k+1时不等式成立.
根据①、②可知:ak≥2对所有n≥2成立.
(2)由递推公式及(1)的结论有
an+1=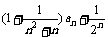 ≤
≤ ,(n≥1)
,(n≥1)
两边取对数并利用已知不等式得
lnan+1≤ln +lnan≤lnan+
+lnan≤lnan+ .
.
故lnan+1-lnan≤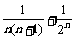 ,(n≥1).
,(n≥1).
上式从1到n-1求和可得
lnan-lna1≤ +
+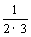 +…+
+…+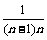 +
+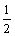 +
+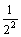 +…+
+…+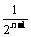
=1-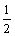 +
+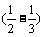 +…
+…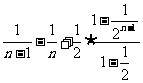 =1-
=1-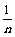 +1
+1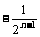 <2,
<2,
即lnan<2,故an<e2 (n≥1).
5.a>b>c,(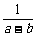 +
+ )(a-c)=(
)(a-c)=(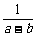 +
+ )[(a-b)+(b-c)]
)[(a-b)+(b-c)]
≥4. ∴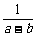 +
+ ≥
≥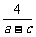 >
>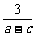 .答案:>; 6. S<1
.答案:>; 6. S<1
4. an+1= ≥
≥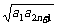 =
= =bn+1.答案:an+1≥bn+1
=bn+1.答案:an+1≥bn+1
6.记S= ,则S与1的大小关系是_________
,则S与1的大小关系是_________
简答:1-3.BAA; 3.当n为正偶数时,a<2-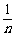 ,2-
,2-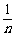 为增函数,
为增函数,
∴a<2-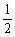 =
= . 当n为正奇数时,-a<2+
. 当n为正奇数时,-a<2+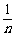 ,a>-2-
,a>-2-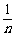 .
.
而-2-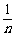 为增函数,-2-
为增函数,-2-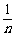 <-2,∴a≥-2.故a∈[-2,
<-2,∴a≥-2.故a∈[-2, )答案:A
)答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com