
17.已知函数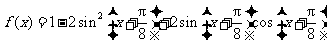 .求:
.求:
(I)函数 的最小正周期;
的最小正周期;
(II)函数 的单调增区间.
的单调增区间.
19. 如图,在四棱锥 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,  ,
, 为
为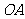 的中点,
的中点,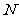 为
为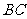 的中点。
的中点。
 (Ⅰ)证明:直线
(Ⅰ)证明:直线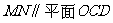
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
18. 甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,且参赛同学的成绩相互之间没有影响,求:
(1)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(2)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
17.已知函数 ,
, .
.
(I)求 的最大值和最小值;
的最大值和最小值;
(II)若不等式 在
在 上恒成立,求实数
上恒成立,求实数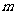 的取值范围.
的取值范围.
19. 在
在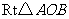 中,
中, ,斜边
,斜边 .
.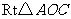 可以通过
可以通过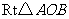 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点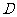 的斜边
的斜边 上.
上.
(I)求证:平面 平面
平面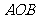 ;
;
(II)当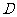 为
为 的中点时,求异面直线
的中点时,求异面直线 与
与 所成角的大小;
所成角的大小;
(III)求 与平面
与平面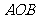 所成角的最大值
所成角的最大值
18. 某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二得奖;摸出两个红球获得一等奖.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.求
(1)甲、乙两人都没有中奖的概率;
(2)甲、两人中至少有一人获二等奖的概率.
17.已知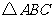 的面积为
的面积为 ,且满足
,且满足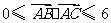 ,设
,设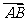 和
和 的夹角为
的夹角为 .
.
(I)求 的取值范围;(II)求函数
的取值范围;(II)求函数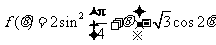 的最大值与最小值.
的最大值与最小值.
19. 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点。
(Ⅰ)求证:EF∥平面SAD;(Ⅱ)设SD = 2CD,求二面角A-EF-D的大小

18. 每次抛掷一枚骰子(六个面上分别标以数字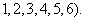
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
17.在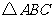 中,
中, ,
, .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若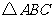 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com