
2、反比例函数 (k不为0)的图象既是
对称图形,又是
对称图形
(k不为0)的图象既是
对称图形,又是
对称图形
1、在式子(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) 中哪些是反比例函数
中哪些是反比例函数
3. 会用反比例函数解决某些实际问题,逐步形成用函数观点处理问题的意识,体验数形结合的思想方法.
复习教学过程设计:
Ⅰ[唤醒]
2. 会画反比例函数的图象,并能根据图象探索并理解反比例函数的性质,进一步提高从函数图象中获取信息的能力.
1. 结合具体情景体会反比例函数的意义,能根据已知条件确定反比例函数的表达式.
4、[实践]
(1)教师自行设计作业。(2)复习指导用书第48页第11题,第53页第12、13题。
第10课时 反比例函数
溧阳市光华初级中学 陈 波
复习教学目标:
(1)下列函数中,表示一次函数的是 ( )
A、 B、
B、 C、
C、 D、
D、
(2)已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )

2、[尝试]
例1、已知一次函数的图象经过点 、
、 ,(1)求函数解析式;(2)画出函数图象;(3)函数的图象经过那些象限?(4)当
,(1)求函数解析式;(2)画出函数图象;(3)函数的图象经过那些象限?(4)当 增大时,
增大时, 的值如何?
的值如何?
解略(答案: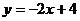 ,图略,图象经过一、二、四象限,
,图略,图象经过一、二、四象限, 随
随 增大而减小)
增大而减小)
例2、已知一次函数
(1)当m、n取何值时,y随x的增大而增大?
(2)当m、n取何值时,直线与y轴的交点在y轴的下半轴?
(3)当m、n取何值时,直线经过一、二、四象限?
分析:(1)一次函数 的性质:当
的性质:当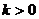 时,
时, 随x的增大而增大;(2)直线
随x的增大而增大;(2)直线 与y轴的交点坐标为
与y轴的交点坐标为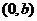 ;(3)当
;(3)当 且
且 一次函数的图象经过一、二、四象限。
一次函数的图象经过一、二、四象限。
解略(答案:(1) ,
, 为一切实数;(2)
为一切实数;(2) ;(3)
;(3)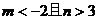 )
)
提炼:利用逆向思维的方法,根据一次函数的性质,体会逆向思维和定向思维的异同。
例3、已知:函数y=(m+1)x+2m﹣6
(1)若函数图象过(﹣1,2),求此函数的解析式。
(2)若函数图象与直线y=2x+5平行,求其函数的解析式。
(3)求满足(2)条件的直线与此同时y=﹣3x+1的交点并求这两条直线与y轴所围成的三角形面积。
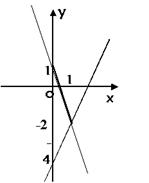 分析:(1)利用函数的表达式与点的坐标的关系;(2)一次函数图象平行,表达式之间的关系;(3)利用点的坐标求线段的长,确定三角形的底和高求三角形的面积。
分析:(1)利用函数的表达式与点的坐标的关系;(2)一次函数图象平行,表达式之间的关系;(3)利用点的坐标求线段的长,确定三角形的底和高求三角形的面积。
解:(1)由题意:2=﹣(m+1)+2m﹣6
解得 m=9 ∴ y=10x+12
(2) 由题意,m+1=2 解得 m=1 ∴ y =2x﹣4
(3) 由题意得
 解得: x=1,y=﹣2 ∴ 这两直线的交点是(1,﹣2)
解得: x=1,y=﹣2 ∴ 这两直线的交点是(1,﹣2)

y=2x﹣4与y轴交于(0,-4) y=﹣3x+1与y轴交于(0,1)
∴S△=
提炼:利用数形结合的思想方法,根据函数的性质结合图形确定函数的解析式及三角形的面积。
 例4、如图,l甲、l乙两条直线分别表示甲走路与乙骑车(在同一条路上)行走的路程S与时间t的关系,根据此图,回答下列问题:
例4、如图,l甲、l乙两条直线分别表示甲走路与乙骑车(在同一条路上)行走的路程S与时间t的关系,根据此图,回答下列问题:
1)乙出发时,与甲相距10km;
2)行走一段时间后,乙的自行车发生故障停下来修理,修车时间为1h;
3)乙从出发起,经过2.5h与甲相遇;
4)甲的速度为5km/h,乙的速度为15km/h;
5)甲行走的路程s(千米)与时间t(小时)之间的函数关系式是s=5t+10(t≥0);
6)在0h<t<2.5h甲走在乙的前面,在t>2.5h甲走在乙的后面;
7)如果乙的自行车不出故障,则乙出发后经过1h与甲相遇,相遇后离乙的出发点15km;在0h<t<1h范围内甲走在乙的前面,在t>1h范围内甲走在乙的后面;并在图中标出其相遇点。(相遇点为A)
提炼:运用函数的图象及性质解决实际问题,并对某些实际问题进行比较、预测,体会生活中的数学。
(1)写出下列函数中自变量 的取值范围。
的取值范围。 ,
, ,
, 。
。
(2)已知 与
与 成正比例,且
成正比例,且 时,
时, ,那么
,那么 与
与 之间的函数关系式为_________________。
之间的函数关系式为_________________。
(3)直线 与
与 轴的交点坐标为(_______),与
轴的交点坐标为(_______),与 轴的交点坐标为(_______)。
轴的交点坐标为(_______)。
(4)根据下列一次函数y=kx+b(k≠0)的草图回答出各图中k、b的符号:

1、[唤醒]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com