3．有一个二次函数，它的图象经过(1，0)；图象的对称轴是x=2；并且它的顶点与x轴的距离是4，则该函数的表达式是(　　　 )

　 A． B. C.D.

Ⅱ. [尝试]

例1.已知二次函数y＝x²+bx+c的图象经过(1，0)与(2，5)两点

(1)　 求这个二次函数的解析式

(2)　 作出该函数的图象，并根据图象回答下列问题：

①　　 函数的对称轴、顶点坐标、与x轴的交点坐标

②　　 当x取何值时，y>0，当x取何值时，y随x的增大而减小？

解略　 (答案： y＝x²+2x－3)

提炼：用待定系数法求二次函数解析式，用描点法作出图象，根据图象解决二次函数的一些基本性质。

例2.函数y＝ax²－ax+3x+1的图象与x轴有且只有一个交点，求a的值和交点坐标，求a的值和交点坐标。

2．抛物线y＝2x²+x－3与x轴两个交点间的距离为(　　 )。

　 A. 2.5　　　 B. －0.5　　　 C. 0.5　　　 D. －2.5

1．二次函数y＝ax²，当a<0时，y的值恒小于0，则自变量x的取值范围(　　 )。

A. x可取一切实数　　　　　　　　　 　B. x>0

C. x<0　　　　　　　　　　　　　　　 D. x≠0

(1)y＝3x－2　 (　　 )　　　　　　　 (2)y＝2x²－3x³　 　(　　 )

(3)y＝1－2x²　 　(　　 )　　　　　　　 (4) y＝　 (　　 )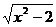

(5)y＝　 (　 　　)　　　　　　　 (6)　 (　　 )

2．抛物线y＝2x²+1的顶点坐标是______，对称轴是　　　　 ，当x＝　　　 时，函数取得最 ___值为　　　　 ；二次函数y＝2x²－8x+1的顶点坐标是______,对称轴是___________,它的图象是由函数y＝2x²+1沿着____轴向____平移______个单位，然后再沿着____轴向____平移______个单位得到。

3．　 理解一元二次方程与二次函数的关系，并能利用二次函数的图象求一元二次方程的近似根，并能利用二次函数的相关知识解决实际问题。

复习教学过程设计

Ⅰ.[唤醒]

2．　 能根据二次函数的表达式确定二次函数的开口方向，对称轴和顶点坐标；会作二次函数的图象，并能根据图象对二次函数的性质进行分析，逐步积累研究函数性质的经验。

1．　 根据具体情境分析和建立两个变量之间的二次函数关系，能用表格、表达式、图象表示变量之间的二次函数关系，并能根据具体问题，选取适当的方法表示变量之间的二次函数关系。

1、　 教师自行设计作业

复习指导用书P₅₈ 19　 、20

第11课　　 二次函数

溧阳市光华中学　 史栋新

　　 复习教学目标