
前面填空部分,并能用所学综合知识解决实际问题。
例1 利用尺规,按下列要求作图,不写作法,保留作图痕迹。
(1) 作出AB的中点M;
(2) 作∠BCD的平分线;
(3) 延长CD到P,使DP=2CD。
分析:本题考查学生用尺规进行基本作图
解:(略)
提炼:本题同时考查了尺规作垂直平分线、作角平分线、作一条线段等于已知线段等知识。
例2
小明的爸爸上街配一块三角形的玻璃,到街上后发现把所量的三边长度弄丢了,打电话问小明,小明却回答他:两边长为30cm和50cm,这两边的夹角为45 。请问:按照这三个数据,他爸爸能配到符合要求的玻璃吗?若能,请按1:10的比例画出这个三角形;若不能,请说明理由。
。请问:按照这三个数据,他爸爸能配到符合要求的玻璃吗?若能,请按1:10的比例画出这个三角形;若不能,请说明理由。
分析:根据“两边及夹角对应相等的三角形全等”,所以能配到符合要求的玻璃。
解:(略)
提炼:这题一方面考查了三角形全等的判定,另一方面帮学生复习1:10作图的含义。
例3
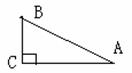 已知Rt△ABC中,∠C=
已知Rt△ABC中,∠C=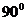 ,用直尺和圆规作图,把它分成两个直角三角形,且要求其中至少一个三角形为等腰三角形(至少两种方法)
,用直尺和圆规作图,把它分成两个直角三角形,且要求其中至少一个三角形为等腰三角形(至少两种方法)
 分析:本题关键是根据等腰三角形的定义想办法得到相等的线段
分析:本题关键是根据等腰三角形的定义想办法得到相等的线段

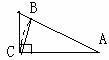 解:(略)
解:(略)



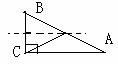
提炼:本题是开放题,考查基本作图方法及一些知识的综合运用。
例4
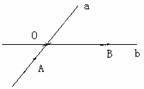 两条公路a、b相交于点O,A、B为两个收购站,请在这块地上找一个仓库P,使仓库到两个收购站的距离相等。
两条公路a、b相交于点O,A、B为两个收购站,请在这块地上找一个仓库P,使仓库到两个收购站的距离相等。

分析:到两点A、B的距离相等的点在线段AB的垂直平分线上,到两边的距离相等的点在交角的平分线上,所以求交点即可。
解:(略)
提炼:本题通过分析题意,运用作垂直平分线和作角平分线找交点,体现数学与生活的联系。
3、 选择:
(1)三角形的外心是 ( )
A、 三条高的交点 B、三条中线的交点
C、三条角平分线的交点 D、三边垂直平分线的交点
(2)到B、C两点的距离相等的点有 ( )
A、一个 B、两个 C、无限个 D、有限个
(3)下列所给条件不能确定一个圆的是 ( )
A、圆心及圆经过的一点 B、圆心及半径 C、圆经过的两点 D、一段圆弧
2、 判断:
(1)画一条直线a,使a=10cm。 ( )
(2)过点A作线段BC的中垂线。 ( )
(3)过三点A、B、C一定能画一个圆。 ( )
(4)过一点一定能作一条已知直线的垂线。 ( )
3、 把一些较复杂的作图问题转化为基本作图问题来解决。
复习教学过程设计:
2、 会用三角板作三角形的高,会用直尺和圆规利用已知条件作一个三角形;会过一点、两点和不在一条直线上的三点作圆;
第19课时 作(画)图
溧阳市第二中学 朱淑芳
复习教学目标:
1、 能用三角板或量角器过一点画已知直线的垂线, 能用三角板、直尺过直线外一点作已知直线的平行线;能用直尺和圆规作一条线段等于已知线段、作一个角等于已知角;作角的平分线;作线段的垂直平分线。了解尺规作图的步骤,对于尺规作图题会写已知、求作和作法(不写证明);
3、解题注意点:在解决问题的过程中,注意解决问题的严密性,充分考虑各种情况。
2、基本数学思想方法:转化的思想;分类讨论的思想;由特殊到一般的思想等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com